Законы динамики впервые точно сформулированы и систематически изложены Исааком Ньютоном в его знаменитых «Математических основах натуральной философии» 1687 года.
Все дальнейшие уравнения динамики выводятся из этих законов при помощи математического анализа.
В современных терминах законы Ньютона могут быть сформулированы следующим образом:
- Закон инерции: Всякая материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит этого состояния.
- Второй закон Ньютона — связь силы, массы и ускорения: Ускорение материальной точки относительно инерциальной системы отсчета пропорционально действующей на точку силе, направлено по этой силе и обратно пропорционально массе точки.
- Закон равенства действия и противодействия: Действие всегда равно и противоположно противодействию, или действия двух тел друг на друга всегда равны и прямо противоположно направлены.
- Закон независимости действия сил: Материальная точка под действием нескольких сил приобретает ускорение, равное геометрической сумме ускорений, которые она получила бы от каждой силы, действующей отдельно, независимо от других.
Следует отметить, что Ньютон сформулировал основные законы динамики для тел, подразумевая под телом свободную материальную точку, т.е. такую точку, на движение которой не наложены какие-либо ограничения, т.е. связи.
1 закон Ньютона — закон инерции
Первый закон Ньютона (его также называют законом инерции) гласит:
«Всякая материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие других тел не изменит этого состояния»
Приведем здесь еще формулировку первого закона динамики, принадлежащую самому Ньютону:
Всякое тело сохраняет состояние покоя или прямолинейного равномерного движения, пока и поскольку приложенные силы не заставят его изменить это состояние.
Первый закон динамики получил название закона инерции в связи с тем, что свойство материальной точки сохранять состояние покоя или равномерного прямолинейного движения при отсутствии взаимодействия с окружающими телами называется инертностью или инерцией точки. Это свойство было указано еще Галилеем.
Система отсчета, по отношению к которой выполняется Ⅰ закон Ньютона, называется инерциальной системой отсчета.
Установлено, что для нашей Солнечной системы с большой степенью точности инерциальной является гелиоцентрическая система отсчета с началом в центре Солнца и осями, направленными на «неподвижные» звезды. Однако при решении большинства практических задач инерциальной системой отсчета можно считать геоцентрическую систему отсчета, неизменно связанную с Землей.
Второй закон Ньютона — связь силы, массы и ускорения тела
Второй закон Ньютона в изначальной формулировке автора гласил:
«Изменение количества движения пропорционально приложенной силе и происходит в направлении силы»
Это главный закон Ньютона, на котором основаны практически все расчеты в инерционной механике и который определяет взаимосвязь между массой тела, его ускорением и силами, действующими на это тело.
Как следует из закона инерции, ускорение материальной точки равно нулю, если точка изолирована от действия сил. Если же к точке приложена некоторая сила, то эта точка отклоняется от инерционного движения, приобретая некоторое ускорение.
Опыт показывает, что одна и та же сила сообщает двум различным покоящимся материальным точкам неодинаковые ускорения.
При действии одинаковых сил модуль ускорения одной материальной точки может оказаться меньшим, чем модуль ускорения другой точки. В этом случае говорят, что первая точка является более инертной, и наоборот. Отсюда следует, что инертность выражает свойство материальной точки под действием силы приобретать в своем движении то или иное ускорение.
Таким образом, ускорения, приобретаемые двумя различными материальными точками, зависят не только от действующих на них сил, но и от инертности этих точек.
Величина, определяющая меру инертности данной материальной точки, называется массой точки.
Масса является величиной скалярной, положительной, и при этом в классической механике она рассматривается как величина постоянная для каждой данной материальной точки.
Масса является единственной характеристикой материальной точки. Отличие материальных точек друг от друга сводится к различию в массах.
Связь между массой m материальной точки, силой F, приложенной к этой точке, и её ускорением a устанавливается вторым законом динамики. Приведем этот закон в следующей формулировке:
Ускорение материальной точки относительно инерциальной системы отсчета пропорционально действующей на точку силе, направлено по этой силе и обратно пропорционально массе точки:
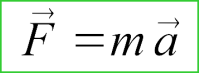
Следует заметить, что из формулировки второго закона динамики не вытекает, что в динамике исследуются движения, происходящие только в инерциальных системах отсчета.
В динамике рассматривается движение и в неинерциальных системах, но только таких, движение которых задано относительно инерциальной системы отсчета.
Формулировка Ⅱ закона Ньютона, в современной трактовке:
Равнодействующая всех сил, приложенных к телу, равна произведению массы этого тела на его ускорение, под действием этих сил.
3 закон Ньютона — закон равенства действия и противодействия
Ⅲ закон Ньютона в первоначальной формулировке гласил:
«Действие всегда равно и противоположно противодействию, или действия двух тел друг на друга всегда равны и прямо противоположно направлены».
В современной трактовке он называется законом равенства действия и противодействия.
Для двух материальных точек Ⅲ закон Ньютона формулируется так:
Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.
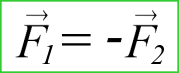
Этот закон широко используется при решении задач раздела «статика» теоретической механики, в частности для определения реакций связей.
Заметим, что силы механического взаимодействия между материальными точками, о которых говорится в третьем законе, приложены к разным материальным точкам и поэтому не уравновешены и могут приводить эти материальные точки в состояние ускоренного движения.
4 закон Ньютона — закон независимости действия сил
Четвертый закон Ньютона называют законом независимости действия сил, и в изначальном виде он гласил:
«От совокупного действия (двух) сил тело описывает диагональ параллелограмма в течение того же времени, как и стороны его при действии сил порознь»
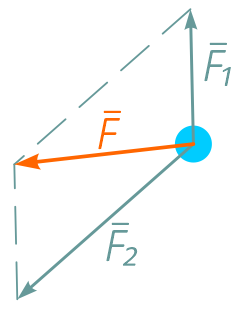
Данная формулировка Ⅳ закона была высказана Ньютоном в примечании к его третьему закону.
Закон независимости действия сил — это аксиома о независимости действия нескольких сил приложенных к одной и той же материальной точке.
В современной формулировке, четвертый закон Ньютона может быть записан так:
Материальная точка под действием нескольких сил приобретает ускорение, равное геометрической сумме ускорений, которые она получила бы от каждой силы, действующей отдельно, независимо от других.
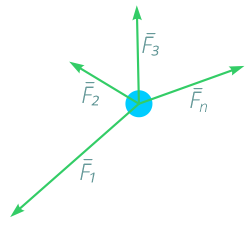
Пусть на материальную точку массой m действуют силы
![]()
Ускорения от каждой из этих сил, действующих отдельно от других —
![]()
Суммируя эти равенства и учитывая, что ускорение a, получаемое точкой от системы сил
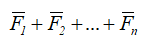
равно
![]()
получаем
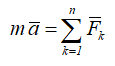
Полученное равенство называется основным уравнением динамики точки в случае действия на точку нескольких сил.
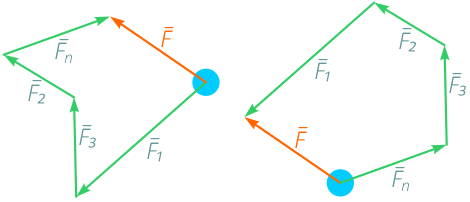
Итак, система сил, приложенных к одной точке, динамически эквивалентна одной силе, равной их геометрической сумме.
Далее: