Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
где a — ускорение точки;
Fi — силы, действующие на точку, включая реакции связей.
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
m∙ ax = ΣFxi
m∙ ay = ΣFyi (2)
m∙ az = ΣFzi
где ax , ay , az — проекции ускорения точки на декартовы оси координат;
Fxi , Fyi , Fzi — проекция i<-той силы на соответствующую ось.
Учитывая, что
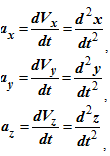
получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки
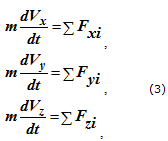
или второго порядка относительно координат точки
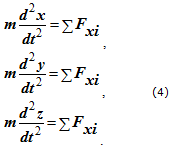
Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений

где aτ и an — касательное и нормальное ускорение точки;
Fτi , Fni , Fbi — проекции i-той силы на касательную, нормаль и бинормаль соответственно.
Учитывая, что
an = V2/ρ,
ab = 0
получим:
mdV/dt = ΣFτi
mV2/ρ = ΣFni (5)
0 = ΣFbi
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
Далее: