Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.

При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.

Статический момент площади

Интегралы вида:

называются статическими моментами площади сечения A относительно осей X и Y соответственно.

В тех случаях, когда сечение может быть разделено на простейшие фигуры площади A_i и координаты центров тяжести x_i и y_i которых известны, статические моменты площади сложной фигуры определяются через суммирование

Статические моменты площади имеют размерность [м³] и могут принимать любые числовые значения. Для осей X_C, Y_C, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:

Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:

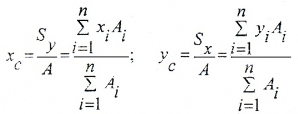
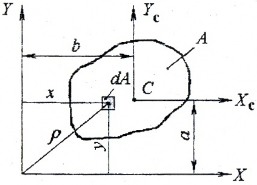
Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.

При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.

Моменты инерции

Моментами инерции площади сечения называют интегралы вида:

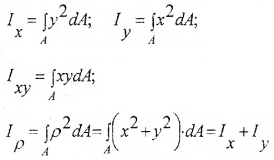
где:
I_x, I_y — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
I_xy — центробежный момент инерции;
I_ρ — полярный момент инерции.

Размерность момента инерции [м⁴], I_x, I_y, I _ρ всегда положительны, I_xy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, I_xy=0.

Зависимости между моментами инерции относительно параллельных осей выражаются формулами:

где a, b – расстояния между осями X, X_C и Y, Y_C.

Оси, относительно которых I_xy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.

Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.

Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (I_max, I_min).

Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:

Радиусы инерции

Величины

называют радиусами инерции сечения относительно осей OX и OY соответственно.

Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции

называют эллипсом инерции.

Лекции по сопромату >
Примеры решения задач >