Проверка правильности построения эпюр изгибающих моментов Mx выполняется по “скачкам” и дифференциальной зависимости dM/dz=Q.
Проверим ранее построенную эпюру Mx.
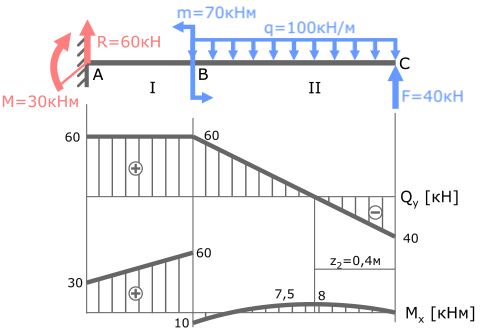
1. Проверка по “скачкам”
В сечениях балки, где приложен изгибающий момент, на эпюре M будет скачок.
Здесь к балке приложено два момента: M в точке A и m в точке B.
Проверим наличие скачков в указанных сечениях:
В точке A изгибающий момент M равен 30кНм.
Скачок значений на эпюре M также равен 30.
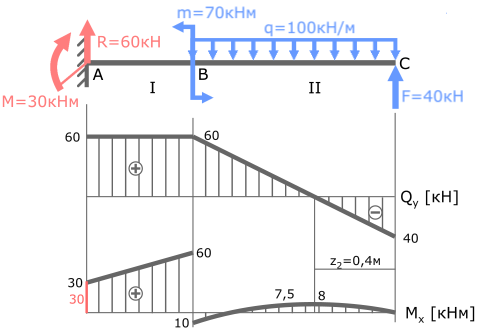
В точке B изгибающий момент m равен 70кНм.
Как видно, скачок значений составляет 70 (от -10 до +60).
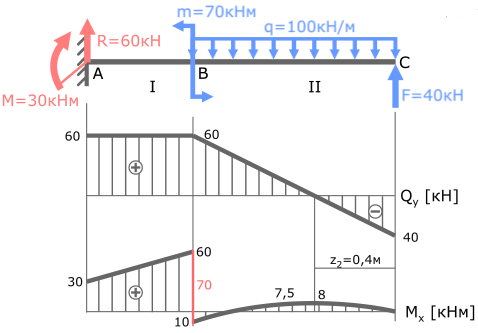
2. Проверка дифференциальной зависимости dM/dz=Q
Выполним проверку эпюры по дифференциальной зависимости dM/dz=Q.
На участках балки, где эпюра Q параллельна базовой линии (I с.у.) эпюра M имеет вид прямой наклонной линии.
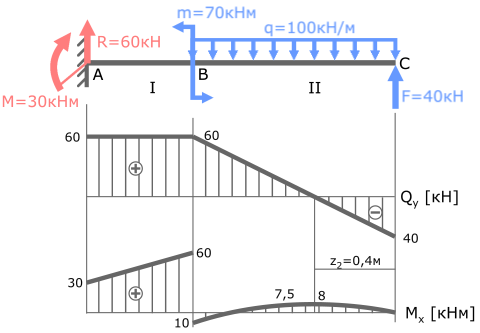
На участках балки с распределенной нагрузкой, где Q≠const (II с.у.) эпюра моментов M имеет вид параболы.
В сечении, где эпюра Q пересекает базовую линию, на эпюре Mx определяется экстремум.
Все условия выполнены, значит, эпюра Mx построена правильно.
Далее: