Пример решения задачи на построение эпюры внутренних изгибающих моментов M_x для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Рассмотрим порядок построения эпюры изгибающих моментов M_x для консольной балки закрепленной в жесткой заделке.

Другие примеры решений >
Помощь с решением задач >

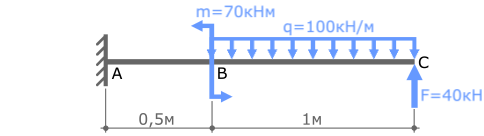
Пример решения

Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Q_y.

Покажем найденные опорные реакции и выбранную систему координат.

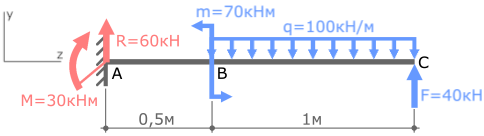
Для построения эпюры изгибающих моментов M_x запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

Другие видео

Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Q_y.

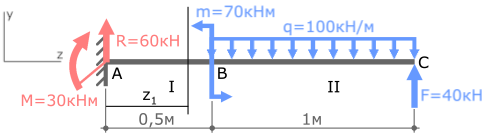
Рассмотрим I силовой участок:

Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.

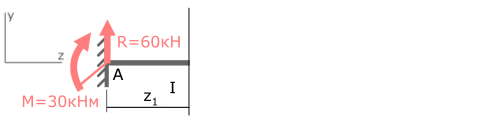
I с.у. (AB) 0 ≤ z₁≤ 0,5м

Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.

Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.

По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:

M_xI=Σm_i=M+R∙z₁=30+60z₁

В выражении переменная z₁ в первой степени, поэтому эпюра M_x на первом участке будет иметь вид прямой линии.

Рассчитаем значения M_xI на границах участка, т.е. при z₁=0 и при z₁=0,5м

M_xI (z₁=0)=30кНм
M_xI (z₁=0,5м)=60кНм

Переходим на второй силовой участок:

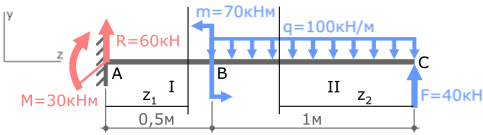
Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.

Эта часть балки изгибается силой F и распределенной нагрузкой q.

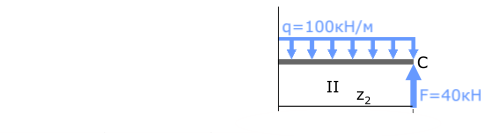
II с.у. (BC) 0 ≤ z₂ ≤ 1м
M_xII=Σm_i=-q∙z₂(z₂/2)+F∙z₂= -50∙z₂²+40∙z₂

Получено выражение с переменной z₂ во второй степени, значит, эпюра M_x на втором участке будет иметь вид параболы.

Видео про построение эпюр:

Другие видео

Для построения параболы требуется как минимум три точки. Этими точками будут значения M_x на границах и в середине II силового участка, то есть при z₂=0, z₂=1м и z₂=0,5м.

M_xII(z₂=0)=0
M_xII(z₂=0,5м)=7,5кНм
M_xII(z₂=1м)= -10кНм

По полученным данным строим эпюру изгибающих моментов M_x (готовую эпюру Q_y перенесем из ранее рассмотренной задачи)

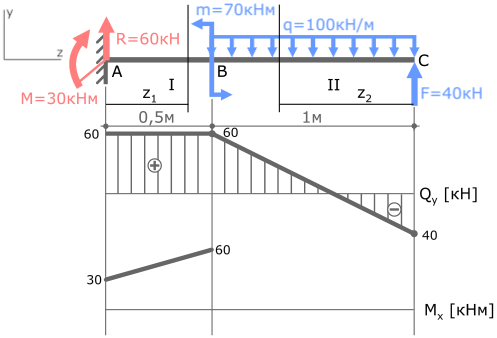
I с.у. (AB) 0 ≤ z₁ ≤ 0,5м.
M_xI=30+60z₁ (прямая)
M_xI(z₁=0)=30кНм
M_xI(z₁=0,5м)=60кНм

II с.у. (BC) 0 ≤ z₂ ≤ 1м
M_xII= -50z₂²+40z₂ (парабола)
M_xII(z₂=0)=0
M_xII(z₂=0,5м)=7,5кНм
M_xII(z₂=1м)= -10кНм

Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Q_y.

Q_y — первая производная от M_x. Поэтому в том месте, где Q_y пересекает базовую линию (т.е. Q_y=0) на эпюре M_x будет экстремум.

Видео про расчет экстремума эпюры:

Другие видео

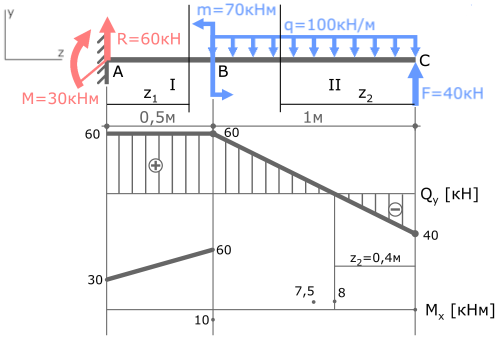
Рассчитаем значение экстремума эпюры M_x на II участке балки.

Для этого:

Отметив эту точку в области эпюры где Q_y=0 соединим ее с тремя другими параболой.

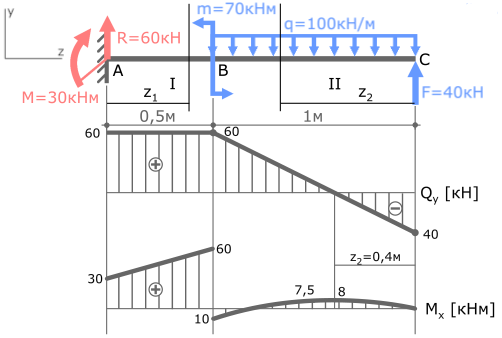
Эпюра изгибающих моментов построена. Проверка эпюры M_x.

Расчеты на прочность >
Другие примеры решения задач >