Пример решения задачи по проверке на прочность стальной стержневой системы из трех сдвоенных уголков при разных допустимых напряжениях на растяжение и сжатие.

Задача

Стержневая система, состоящая из трех одинаковых стержней разной длины, нагружена сосредоточенной силой F=100кН приложенной горизонтально в точке B.

Другие примеры решений >
Помощь с решением задач >

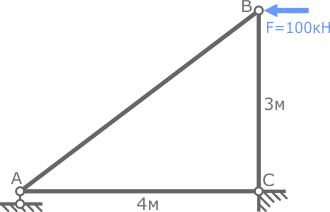
Все стержни системы состоят из двух равнополочных уголков 80×8мм.

Допустимые напряжения для материала стержней:

• на растяжение [σ_р]=50МПа,
• на сжатие [σ_сж]=120МПа.

Требуется: проверить стержневую систему на прочность.

Решение

Как известно, система считается прочной, только если прочны все составляющие ее элементы.

Поэтому в данной задаче, для проверки на прочность требуется определить напряжения во всех трех стержнях системы и сравнить полученные значения с соответствующими допустимыми.

Другими словами, напряжения в растягиваемых стержнях должны быть не больше допустимых на растяжение, а в сжимаемых соответственно не больше [σ_сж].

Под действием внешней силы, стержни, очевидно, испытывают продольное нагружение (растяжение либо сжатие), следовательно, для расчета напряжений используем соответствующие условия прочности:

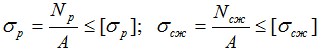
Площадь поперечного сечения A всех стержней одинакова. Рассчитаем ее.

Для этого по сортаменту прокатной стали для равнополочных уголков найдем площадь сечения одного уголка и удвоим ее значение (т.к. стержни состоят из двух уголков):

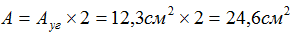
Внутренние продольные усилия в стержнях составляют:

N_AB=125кН (сжатие)
N_BC=75кН (растяжение)
N_AC=100кН (растяжение)

Расчет внутренних сил в стержнях данной системы подробно показан здесь.

Осталось рассчитать напряжения в стержнях и сравнить их с соответствующими допустимыми значениями.

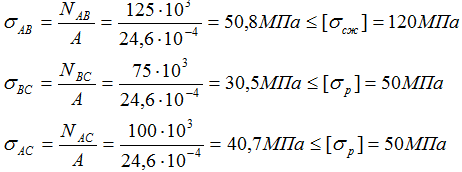
Так как напряжения во всех стержнях системы не превышают соответствующих допустимых значений система является прочной.

Другие примеры решения задач >