Рассмотрим общее уравнение динамики механической системы в обобщенных силах и его частные случаи:

При изменении всех обобщенных координат приращение радиуса-вектора (рисунок 3.1, г) складывается из приращений, соответствующих изменению каждой обобщенной координаты:

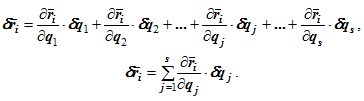
С учетом этого выражения общее уравнение динамики можно записать:

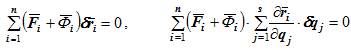
Поменяв порядок суммирования, получим

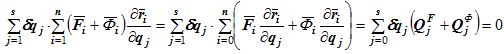
где δq_j — принимаемое нами приращение обобщенной координаты, не равное нулю. Следовательно,

Q_j^F + Q_j^Φ = 0,   i,…j,…s.

То есть получаем систему из s уравнений, которые и называют общим уравнением динамики в обобщенных силах.

Если механическая система находится в равновесии, то силы инерции отсутствуют, получаем принцип возможных перемещений в обобщенных силах:

Для равновесия консервативной системы с учетом формулы (3.3) получим

Примеры решения задач >
Уравнения Лагранжа второго рода >