Третья форма условий равновесия плоской системы сил гласит: алгебраическая сумма моментов всех сил относительно двух любых точек A и B равна нулю и сумма проекций этих сил на ось Ox, не перпендикулярную к прямой, проходящей через точки A и B, тоже равна нулю,

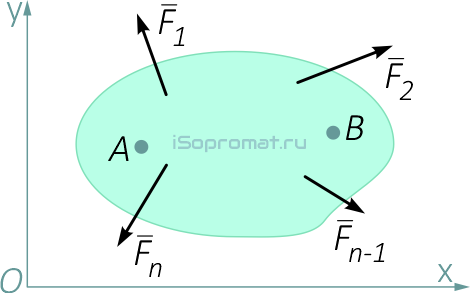
т.е. должны выполняться следующие три условия:

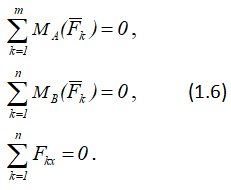
Необходимость этих условий, так же как и в предыдущем случае, следует из первой формы условий равновесия. Докажем их достаточность, т.е. докажем, что если выполняются условия (1.6), то рассматриваемая плоская система сил находится в равновесии.

Выполнение первых двух условий (1.6) означает, что главный момент данной системы сил относительно центров приведения A и B равен нулю.

Такая система может иметь равнодействующую, приложенную в центре приведения, и при R*≠0 линия действия равнодействующей проходит через точки A и B (рисунок 2.2).

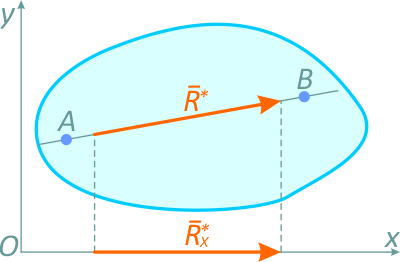
Но по третьему условию из (1.6) проекция равнодействующей на ось Ox равна нулю. Так как ось Ox (рисунок 2.2) не перпендикулярна AB, то это последнее условие может быть выполнено только в случае, если R*=0, т.е. когда рассматриваемая система сил уравновешена.

В частном случае, если линии действия всех сил плоской системы параллельны (плоская система параллельных сил), то условия равновесия таких сил выражаются не тремя, а двумя уравнениями:

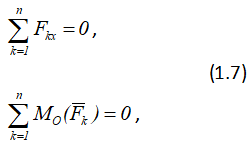
причем ось Ox параллельна данным силам, или

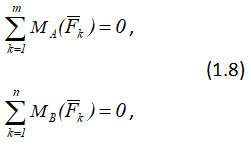
при этом прямая AB не параллельна данным силам.

Дополнительно: