Рассмотрим уравнения Лагранжа второго рода для механической системы имеющей две степени свободы:
В случае если механическая система имеет две степени свободы (s = 2), положение этой системы определяется двумя обобщенными координатами q1 и q2, которым соответствуют обобщенные силы Q1 и Q2.
Уравнения Лагранжа второго рода для такой системы будут выглядеть так
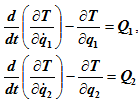
В случае если система является консервативной (т.е. все активные силы, действующие на систему, являются потенциальными), то уравнения Лагранжа второго рода для такой системы будут иметь вид
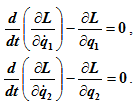
Для решения задач часто более удобна эквивалентная форма записи:
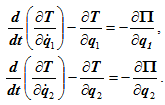
Чтобы составить уравнения Лагранжа второго рода для системы с двумя степенями свободы, следует действовать в такой последовательности:
- сделать рисунок, обозначить на нем все активные силы, приложенные к системе;
- выбрать обобщенные координаты q1 и q2. Рекомендации по выбору обобщенной координаты для случая системы с одной степенью свободы остаются в силе и для этого случая;
- определить, является ли рассматриваемая система консервативной;
- если система является консервативной, следует вычислить ее кинетическую T и потенциальную Π энергии, выразив их через обобщенные координаты q1 и q2 и обобщенные скорости q1‘ и q2‘. Если система не является консервативной, следует вычислить только ее кинетическую энергию;
-
вычислить производные, входящие в уравнения Лагранжа второго рода.
Если система неконсервативная, это будут производные
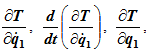
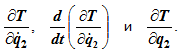
Если система консервативная, к ним добавятся производные
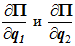
- определить обобщенные силы Q1 и Q2. Способ определения обобщенной силы описан выше (пункт 3.2). Если система консервативная, этот пункт следует пропустить;
- все найденные производные и обобщенные силы подставить в уравнения Лагранжа второго рода для системы с двумя степенями свободы, в формулировке для консервативной или неконсервативной системы.
Далее: