Теорема Вариньона гласит: момент равнодействующей системы сил относительно какого-либо центра равен геометрической сумме моментов составляющих систему сил относительно того же центра.
В некоторых случаях при определении момента силы возникают трудности в расчете плеча силы.
Теорема Вариньона значительно упрощает решение этого вопроса.
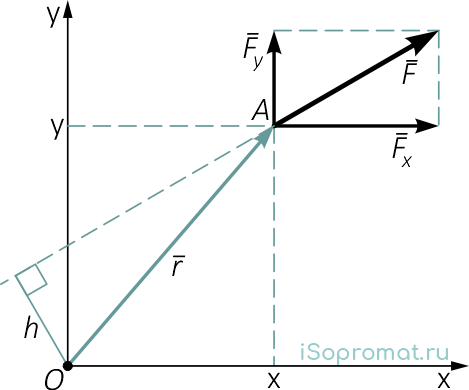
Например, момент силы F относительно точки O можно определить как алгебраическую сумму моментов сил Fx и Fy (на которые можно разложить силу F) относительно той же точки O (рисунок 1). То есть
![]()
где Fx, Fy, x и y – проекции на оси координат силы F и радиус-вектора r.
Применение теоремы Вариньона при решении задач
Рассмотрим способ использования теоремы Вариньона на примере выполнения РГР 1 — равновесие тела под действием произвольной плоской системы сил.
Задача
Жесткая рама закреплена в точке A шарнирно, а в точке B прикреплена к невесомому стержню с шарнирами на концах.
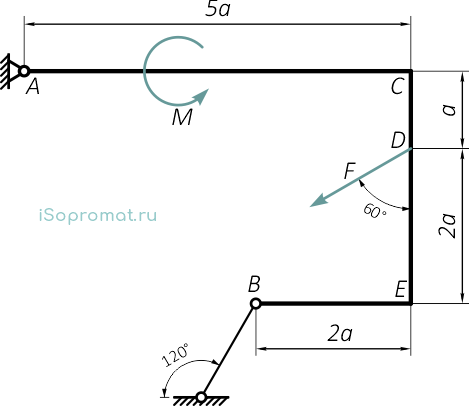
На раму действует пара сил с моментом М=20 кНм и сила F=10 кН приложенная под углом 60° от вертикали, направления и точки приложения которых показаны на расчетной схеме.
Требуется определить реакции связей в точках A и B, вызываемые действующими нагрузками. При окончательных расчетах принять a=1 м.
Решение
Уравнение моментов будет более простым (содержать меньше неизвестных), если записать сумму моментов относительно точки, где пересекаются линии действия двух неизвестных реакций связей.
При вычислении момента силы F часто удобно разложить ее на составляющие Fx и Fy для которых плечи сил легко определяются, и воспользоваться теоремой Вариньона, тогда МOF = МOFx+ МOFy.
Рассмотрим равновесие жесткой рамы.
Проведем координатные оси x-y и покажем действующие на раму усилия: реакции связей RAx и RAy в точке A (неподвижной шарнирной опоре) и реакцию стержня RB в точке В.
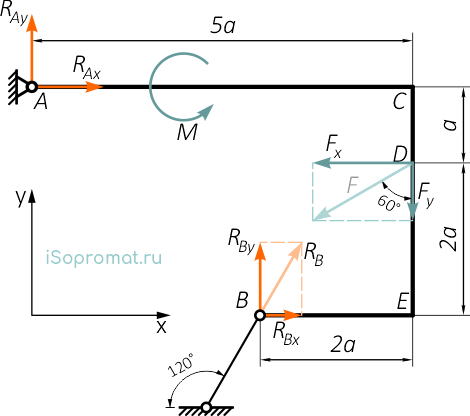
При вычислении моментов силы F и реакции RB воспользуемся теоремой Вариньона, т.е. раскладываем силы на составляющие (проекции сил на оси координат).
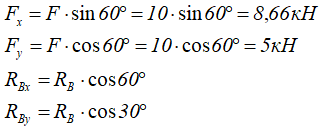
Для полученной плоской системы сил можно составить три уравнения равновесия:
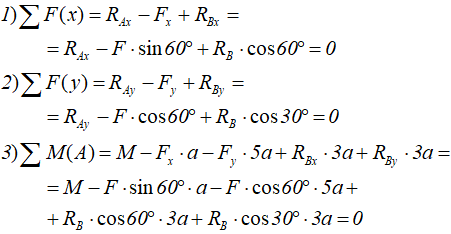
Из уравнения (3) получаем величину RB:
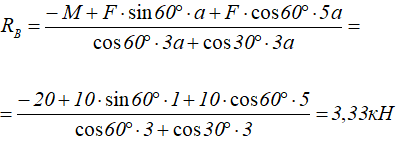
Из уравнения (1) находим RAx:
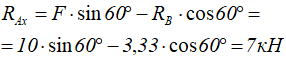
Из уравнения (2) определяем RAy:
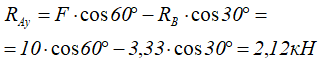
Полная реакция шарнирно-неподвижной опоры определяется по формуле:
![]()
Ответ: RA=7,3 кН, RB=3,33 кН
Далее: