Пример решения задачи по определению угловой скорости кривошипа в зависимости от угла его поворота, для эпициклического механизма, приводимого в движение с помощью постоянного вращающего момента из состояния покоя.
Задача
Эпициклический механизм, расположенный в горизонтальной плоскости, приводится в движение из состояния покоя с помощью постоянного вращающего момента Mвр, приложенного к кривошипу OA (рисунок 4.2).
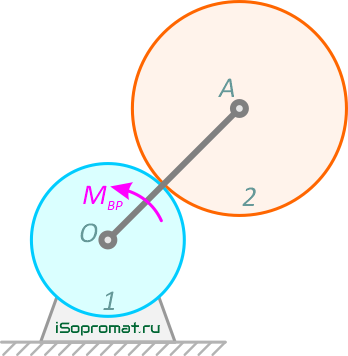
Определить угловую скорость кривошипа ω в зависимости от угла поворота φ, если радиус неподвижного колеса 1 равен r1, радиус колеса 2 – r2, вес колеса 2 равен G, вес кривошипа – P. Колесо 2 считать однородным диском, кривошип – однородным стержнем.
Пример решения
В данной механической системе кинетической энергией обладают колесо 2 (T2) и кривошип OA (TOA), работу совершает вращающий момент на угловом перемещении φ.
Согласно теореме об изменении кинетической энергии
![]()
где T=T2+TOA;
T0=0 (т.к. в начальный момент времени система находилась в покое);
Кинетическая энергия кривошипа
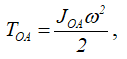
момент инерции кривошипа относительно оси O
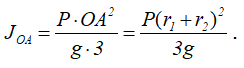
Тогда
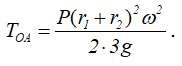
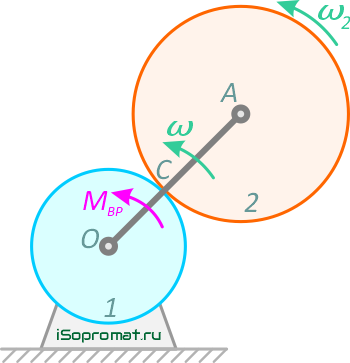
Колесо 2 совершает плоскопараллельное движение, одновременно участвуя в двух вращениях вокруг параллельных осей O и A в одном направлении. Мгновенная ось проходит через точку C параллельно осям O и A. Следовательно,
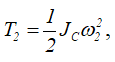
где по теореме Штейнера-Гюйгенса
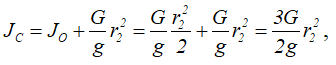
угловая скорость колеса 2
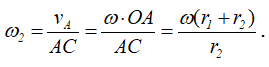
Таким образом,
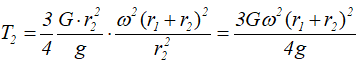
и, следовательно,
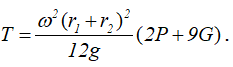
Итак,
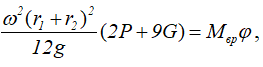
откуда получаем выражение для определения угловой скорости кривошипа
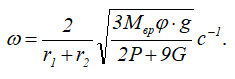
Далее: