Пример решения задачи по определению угла отклонения стержня от вертикали при его вращении как функцию угловой скорости и реакций опор в заданных точках.

Задача

С невесомым валом AB шарнирно скреплен однородный стержень OD длиной l и массой m₁, имеющий на конце груз массой m₂.

Вал и стержень вращаются вокруг оси OZ с постоянной угловой скоростью ω. Известны b₁ и b₂ – расстояния от опор до точки крепления стержня (рисунок 1.4).

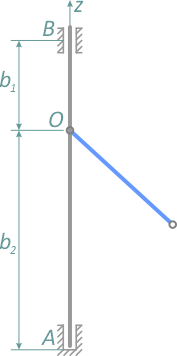
Требуется определить угол отклонения стержня от вертикали — α, как функцию угловой скорости и реакции опор A и B.

Решения других задач

Решение

Применим принцип Даламбера для данной системы. Проведем вращающиеся вместе с валом и стержнем оси координат Axyz так, чтобы стержень OD находился в плоскости yAz. Внешние силы: G₁, G₂; реакции опор: x_A, y_A, z_A, x_B, y_B; силы инерции Φ₁ и Φ₂ (рисунок 1.5).

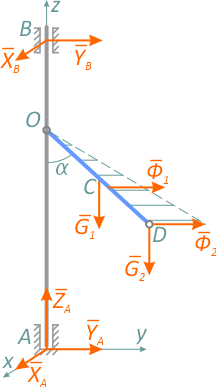
Отклонение стержня от вертикали происходит за счет сил инерции. Определенной угловой скорости соответствует свой угол отклонения. Величина силы инерции стержня определяется из формулы

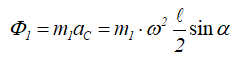
и направлена перпендикулярно к оси вращения, в сторону, противоположную ускорению центра масс стержня.

Эпюра распределения сил инерции стержня представляет собой треугольник (элементарные силы инерции частичек стержня возрастают с удалением от точки O к точке D, т.к. растет их ускорение с увеличением радиуса вращения). Результирующая таких сил приложена на расстоянии 2/3 длины стержня от точки O (см. раздел «Статика», распределенные нагрузки).

Сила инерции точечной массы

Напишем для равновесия стержня при данной угловой скорости ω уравнение моментов относительно точки O – точки крепления стержня:

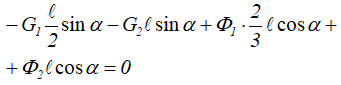
подставляем данные:

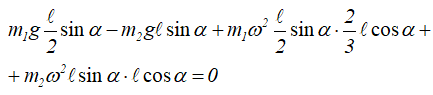
определяем угол:

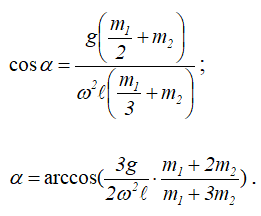
Для определения реакций опор вала составим уравнения равновесия:

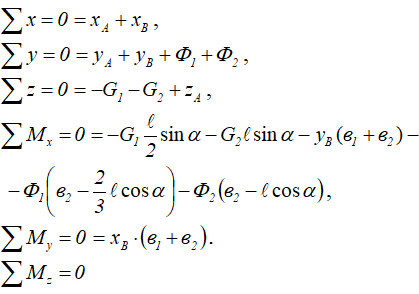
— вращающие моменты отсутствуют, система вращается по инерции, с постоянной угловой скоростью.

Из имеющихся пяти уравнений, подставляя данные задачи, можно найти пять неизвестных реакций в опорах A и B.

---

Далее: