Пример решения задачи по расчету угловой скорости и углового ускорения конуса, который катится по неподвижной горизонтальной плоскости без скольжения, а также, скорости и ускорения нижней и верхней точек его основания.

Задача

Конус с углом при вершине 2α = 60° и радиусом основания r = 20 см катится по неподвижной горизонтальной плоскости без скольжения (Рисунок 5). Скорость центра основания постоянна, V_C = 60 см⁄с.

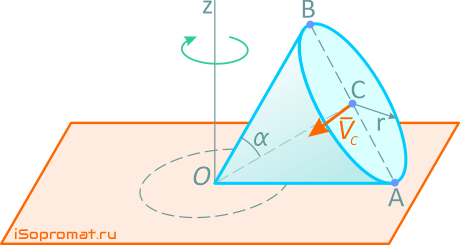
Рисунок 5

Требуется определить:

1. угловую скорость конуса ω;
2. угловое ускорение конуса ε;
3. скорости нижней и наивысшей точек основания V_A и V_B;
4. ускорения этих же точек a_A и a_B (рисунок 5).

Теория по теме задачи

Решение

Определение угловой скорости конуса

Рассматриваемое движение конуса является сферическим, так как его вершина остается неподвижной.

Так как конус катится по неподвижной плоскости, то образующая OA, которой он соприкасается с плоскостью, является мгновенной осью вращения, т.е. все точки этой образующей имеют нулевую скорость.

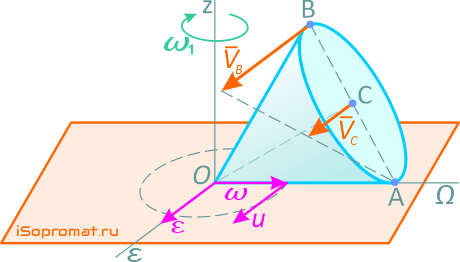
Рисунок 6

Зная скорость точки C, можно сразу определить угловую скорость конуса. Найдем расстояние от C до мгновенной оси (рисунок 7):

Определяем угловую скорость:

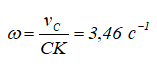
Учитывая направление вектора V_C, откладываем вектор ω от точки O вдоль мгновенной оси так, чтобы смотря ему навстречу, видеть вращение конуса происходящим против движения часовой стрелки:

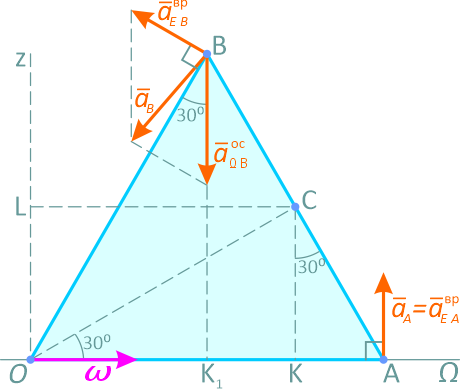
Рисунок 7

Расчет углового ускорения конуса

Для определения углового ускорения ε необходимо построить годограф угловой скорости ω. При качении конуса по горизонтальной плоскости вектор ω перемещается в этой плоскости, поворачиваясь вокруг вертикальной оси z. Так как модуль его не изменяется, то конец вектора ω описывает окружность в горизонтальной плоскости.

Вектор ε геометрически равен скорости u конца вектора ω. В данном случае скорость u является вращательной вокруг оси z. Угловая скорость этого вращения ω₁ определяется как угловая скорость вращения оси конуса OC вокруг оси z. Чтобы определить ее модуль, находим расстояние от точки C до оси z:

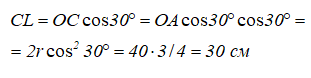
Определяем ω₁:

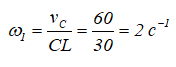
Скорость u находим как вращательную скорость точки – конца вектора угловой скорости ω при вращении вокруг оси z:

Вектор ε отложен от неподвижной точки в направлении скорости u, т.е. лежит в горизонтальной плоскости и перпендикулярен вектору ω.

Расчет скоростей точек основания

Определим скорости точек A и B. Точка A лежит на мгновенной оси вращения, ее скорость равна нулю V_A = 0.

Скорость точки B (рисунок 7):

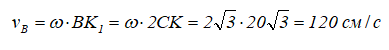
Вектор скорости V_B направлен перпендикулярно плоскости ΩOz.

Вычисление ускорений точек

Точка B имеет ускорение a_B, равное сумме осестремительного ускорения a_ΩB^ос и вращательного ускорения a_EB^вр:

По формулам находим:

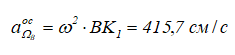
Для определения модуля a_EB^вр опустим из B перпендикуляр на ось углового ускорения E. Этот перпендикуляр совпадает с отрезком BO (рисунок 6).

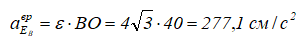
Направляем a_EB^вр перпендикулярно BO в плоскости, перпендикулярной ε так, чтобы, смотря навстречу ε, видеть вектор a_EB^вр, направленным против часовой стрелки.

Определяем модуль a_B как длину диагонали параллелограмма:

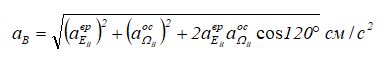
В точке A, лежащей на мгновенной оси вращения, осестремительное ускорение равно нулю: a_ΩA^ос = 0. Определяем модуль вращательного ускорения точки A (рисунок 7):

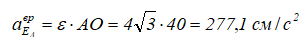
Вектор a_EA^вр направлен перпендикулярно AO в плоскости ΩOz.

---

Далее: