Вторая основная задача динамики точки обратна первой, и заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.

Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.

Уравнение второго основного закона динамики для материальной точки массой m запишется в виде

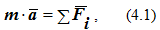
где a – ускорение точки;
F_i – силы, действующие на точку, включая реакции связей.

Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений

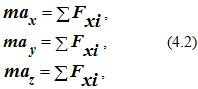
где a_x , a_y , a_z – проекции ускорения точки на декартовы оси координат;
F_x , F_y , F_z – проекция i-й силы на соответствующую ось.

Учитывая, что

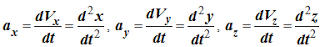
получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки или второго порядка относительно координат точки.

Спроектировав уравнение (4.1) на естественные оси координат, получим следующую систему уравнений:

Учитывая, что

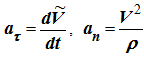
где V – алгебраическое значение скорости точки, получим

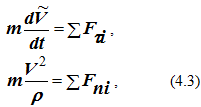
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых, или в естественных координатах.

Каждое дифференциальное уравнение дает целый класс решений, отличающихся друг от друга на некоторую постоянную величину.

Чтобы получить решение конкретной задачи, должны быть заданы так называемые начальные условия, которые позволяют определить постоянные интегрирования.

Примеры решения задач >
Дифференциальные уравнения относительного движения материальной точки >