Решение задачи (РГР) К3 «Кинематический анализ плоского механизма» по разделу «кинематика» теоретической механики.
Пример определения в заданном положении, скоростей и ускорений точек твердого тела при плоском движении.
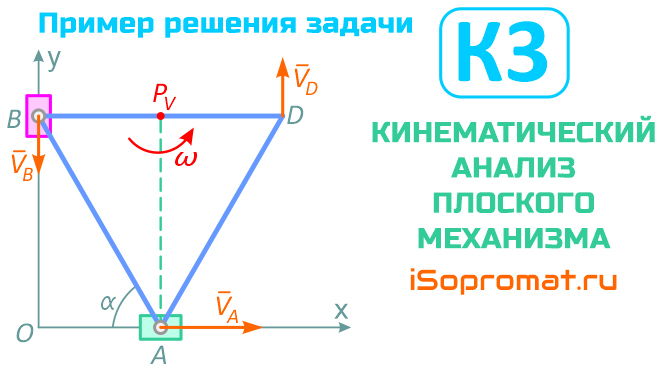
Задача
Вершины A и B равностороннего треугольника ABD перемещаются соответственно по осям OХ и OY. Известны: размер АB = 40 см, скорость VA = 4√3 м/с, ускорение aA = 100 м/с2 и угол α = 60°.
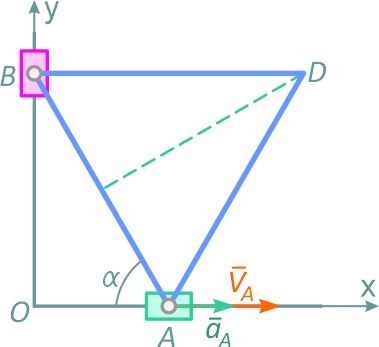
Рисунок 21
Требуется провести кинематический анализ плоского механизма и определить скорости и ускорения точек B и D треугольника в заданном положении.
Решение
Кинематический анализ и определение скоростей точек
Проводим кинематический анализ механизма:
1) По теореме о скоростях точек в плоскопараллельном движении:
![]()
Направление и величина скорости точки А, VA известны, скорость точки B направлена вдоль оси OY, а скорость VBA перпендикулярна стороне АВ.
Строим равенство (1) (см. рисунок 22).
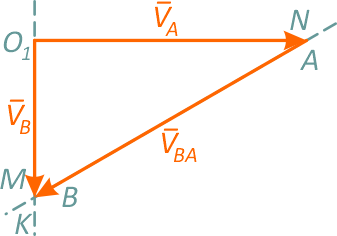
Рисунок 22
Из точки О1, параллельно оси ОХ, вдоль которой движется точка А, откладываем в масштабе вектор VA. Из конца вектора VA проводим линию MN перпендикулярно стороне треугольника AB (60° с вертикалью), тогда пересечение линии O1K параллельно оси OY и MN обозначит вектор VB.
Полученный треугольник скоростей соответствует формуле (1). Умножив масштаб на длины векторов, получим их величины.
Если рисунок 22 строится без соблюдения масштаба, то определение величин скоростей производится с помощью теоремы синусов:
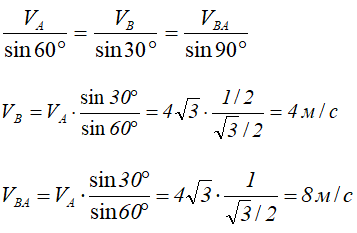
Поскольку VBA = ωAB × AB, то может быть определена угловая скорость вращения точки B вокруг A (или, что то же самое, угловая скорость вращения треугольника ABD).
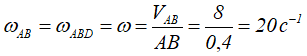
В данном примере не известно направление скорости точки D. Поэтому для определения скорости точки D пишем:
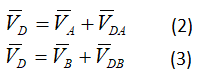
Аналогично (рисунок 22) делаем построение для определения скорости точки D (рисунок 23).
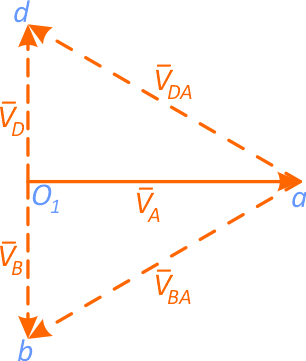
Рисунок 23
Линия ad перпендикулярна стороне треугольника AD, bd перпендикулярна BD. Точка D – точка пересечения линии ad и bd определяет конец вектора, проведенного из точки O1; отрезок ad соответствует вектору VDA, bd – вектору VDB. При известных углах можно определить величину скорости VD точки D.
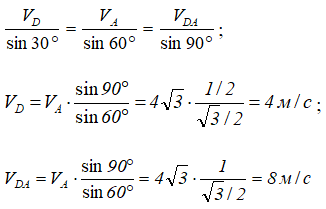
2) Определение скоростей точек с помощью мгновенного центра скоростей.
Мгновенный центр скоростей звена AB — PV находится в точке пересечения перпендикуляров к скоростям точек (см. рисунок 24) – (АPV ⊥ VA, BPV ⊥ оси OY, вдоль которой направлена скорость точки B), после нахождения МЦС — можно написать соотношение
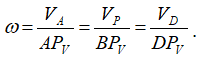
Направление вращения треугольника определяем по вращению точки A вокруг точки PV (в данном случае против хода часовой стрелки).
Величина угловой скорости треугольника
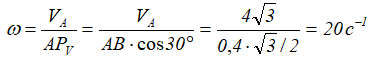
Далее определяем величины скоростей других точек:
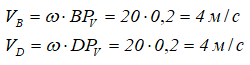
Векторы скоростей перпендикулярны соответствующим отрезкам BPV и DPV, и направлены в сторону вращения.
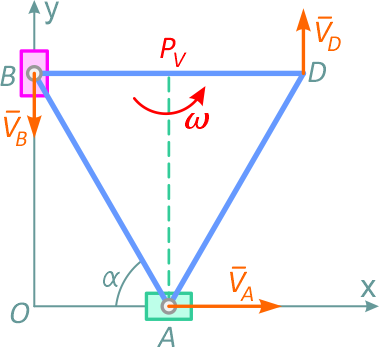
Рисунок 24
Определение ускорений точек
1) Ускорение точки B определяется по формуле
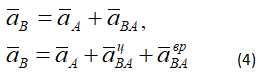
Ускорение точки A задано, т.е. известно по величине и направлению; ускорение aцAB направлено от точки B к точке A и вычисляется по формуле
![]()
Известно также, что вектор aB направлен вдоль оси OY, т.к. точка B движется вдоль этой оси, а вектор aврAB направлен перпендикулярно линии AB. С учетом сказанного можно построить эти векторы (рисунок 25а) или построить равенство (4) (рисунок 25б) и спроецировать его на выбранные оси координат BX1 и BY1:
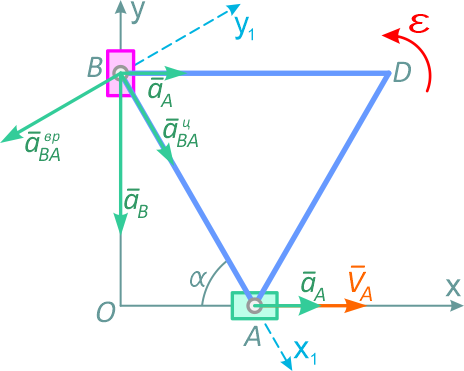
Рисунок 25а
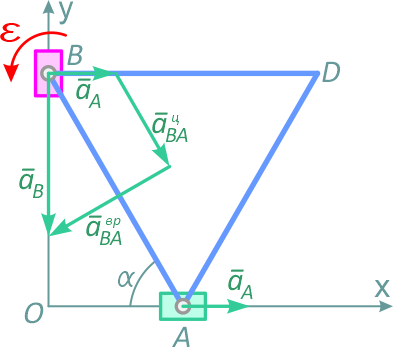
Рисунок 25б
проекции на ось BX1
![]()
на ось BY1
![]()
или
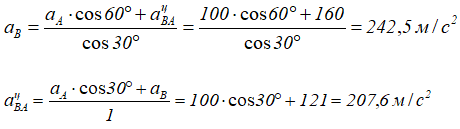
Оба ускорения aB и aврBA оказались положительными. Это значит, что предварительный выбор направления (рисунок 25а) оказался верным.
Из формулы
![]()
можно определить угловое ускорение треугольника (или точки B при вращении вокруг точки A):
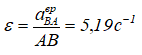
Направление углового ускорения определяется вектором aврBA. В данном примере видно, что точка B, вращаясь вокруг A, ускоряется против хода часовой стрелки.
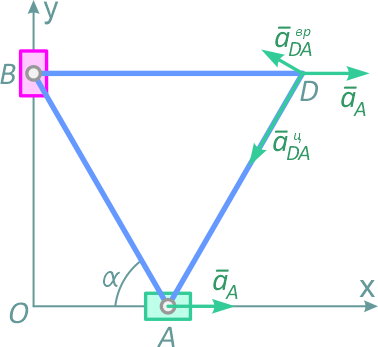
Рисунок 26
2) Ускорение точки D определяется по формуле (см. рисунок 26)
![]()
В этой формуле известны слагаемые правой части:
![]()
Этот вектор направлен от точки D к выбранному полюсу A.
Вектор aврDA перпендикулярен отрезку AD и направлен соответственно угловому ускорению ε треугольника ABD. Так как и величина и направление ускорения точки D неизвестны, то векторное равенство (5) проецируем на выбранные оси координат (OX и OY).
Получим:
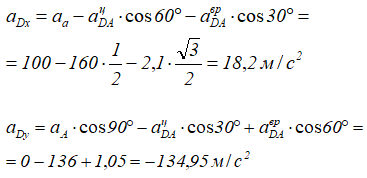
Полное ускорение точки D:
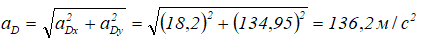
Направление ускорения точки D определяется с помощью направляющих косинусов:
cos α – косинус угла между вектором ускорения и осью OX:
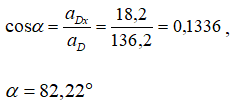
cos β — косинус угла между вектором ускорения и осью OY:
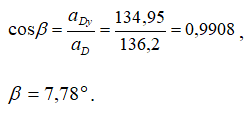
Кинематический анализ плоского механизма завершен.
Далее: