Деформация балки при изгибе проявляется в искривлении ее продольной оси.
Рассмотрим это на примере простой консольной балки, нагруженной изгибающим моментом m.
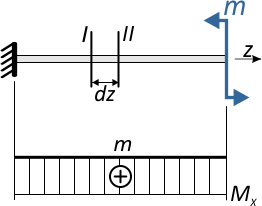
Мысленно вырежем из балки фрагмент длиной dz.
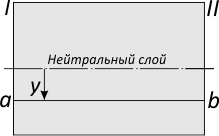
на котором отметим нейтральный слой и отрезок ab соединяющий сечения I-II и равноудаленный от нейтрального слоя на расстояние y.
От действия изгибающего момента данный фрагмент изогнется вместе с балкой
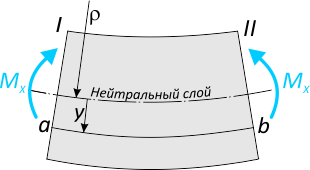
Кривизна рассматриваемого фрагмента балки определяется как
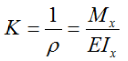
где
ρ – радиус кривизны изогнутой оси балки в данном сечении;
Mx — изгибающий момент в сечении;
E – модуль Юнга материала балки;
Ix — осевой момент инерции поперечного сечения.
Вследствие деформации, поперечные сечения балки, на всех участках, где есть изгибающий момент, повернутся относительно нейтральной оси (линии) на некоторый угол.
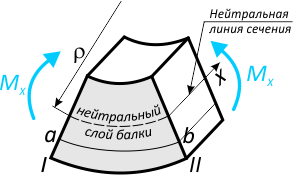
Из-за этого, все слои балки кроме нейтрального будут растягиваться или сжиматься.
В данном примере верхние слои балки сжаты, нижние – растянуты.
Относительное удлинение отрезка (слоя) ab
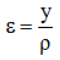
В общем случае нагружения искривление продольной оси упругой линии балки описывается дифференциальным уравнением следующего вида
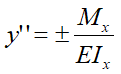
непосредственное интегрирование которого позволяет рассчитывать угловые и линейные перемещения сечений балки при изгибе.
Далее: