Лабораторная работа №14 по испытанию на устойчивость прямого стального стержня при его продольном изгибе.
Цель работы – исследовать явление потери устойчивости прямолинейной формы равновесия при осевом сжатии, проверить опытным путем справедливость формулы Эйлера.
Основные сведения
У стержней, длина которых значительно больше поперечных размеров, при определенной величине осевой сжимающей силы происходит искривление оси. Это явление носит название продольного изгиба. Переход прямолинейной формы равновесия в криволинейную называется потерей устойчивости.
Сжимающая сила, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической. Ее можно определить по формуле Эйлера
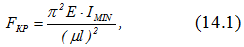
где Е – модуль продольной упругости материала;
l – длина стержня;
Imin – минимальный момент инерции сечения;
μ – коэффициент приведения длины, который зависит от способов закрепления концов стержня.
Формула Эйлера применима лишь в том случае, если потеря устойчивости стержня происходит при напряжениях, меньших предела пропорциональности σпц, т.е. когда справедлив закон Гука
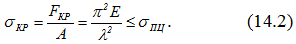
Здесь А – площадь поперечного сечения;
λ=μ∙l/imin – гибкость стержня;

– минимальный радиус инерции сечения.
Предельная гибкость, начиная с которой можно использовать формулу Эйлера, определяется по формуле
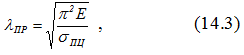
зависит лишь от физико-механических свойств и является постоянной для данного материала.
Так, например, для стали Ст.З λпр = 100, для древесины λпр = 110, для чугуна λпр = 80, для дюралюминия λпр = 60.
Стержни, у которых λ > λпр, называются стержнями большой гибкости.
При меньших значениях гибкости (стержни средней гибкости) критические напряжения σкр > σпц определяются по эмпирическим формулам или соответствующим им таблицам (графикам). Например, формула Ясинского для определения критических напряжений имеет вид
где a и b – эмпирические коэффициенты.
Например, для стали Ст.3 a = 310 МПа, b = 1,14 МПа, для древесины (сосна) a = 28,7 МПа, b = 0,19 МПа.
Эмпирические формулы, особенно для древесины, дают лишь приближенный результат.
Для стержней малой гибкости, у которых σкр, подсчитанные по формуле Ясинского, получаются больше, чем опасные (предельные) напряжения, принимают:
σкр = σт – для пластичных материалов;
σкр = σпч – для хрупких материалов.
Порядок выполнения и обработка результатов
Опыты по исследованию устойчивости сжатых стержней производятся либо на испытательных машинах малой мощности (Р-5 и других), либо на специальных установках, например, СМ-20.
На испытательных машинах величина критической силы определяется непосредственно по шкале динамометра.
На установке СМ-20 (рис. 14.1) нагружение производится с помощью винтовой пары (подъемный винт-гайка) через тарированную пружину; величина нагрузки определяется по осадке пружины δ, которая пропорциональна сжимающей силе:
F = С · δ,
где С – жесткость пружины, определяется из тарировочного графика.
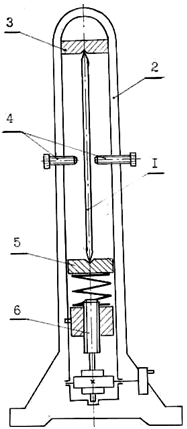
Рис. 14.1. Схема установки СМ-20:
4 – ограничительные упоры;
5 – нижняя опора; 6 –силовое устройство
Установка СМ-20 позволяет определить критическую силу для стержня с шарнирно опертыми концами (μ = 1).
Порядок проведения испытаний и обработки результатов следующий.
- Измеряем длину и размеры поперечного сечения образца, определяем геометрические характеристики сечения и гибкость стержня (Imin, A, imin, λ).
- Сравниваем значения λ и λпр, выясняем, по какой формуле следует определять критическую силу.
- Вычисляем теоретическое значение критической силы.
- Устанавливаем стержень на опорах установки.
- Упоры при помощи винтов устанавливаем примерно на одинаковых расстояниях (2 – З мм) от испытуемого образца.
- Производим нагружение стержня путем плавного и медленного вращения маховика по часовой стрелке, с возрастанием нагрузки нужно непрерывно следить за поведением образца.
Если при F < Fкр слегка изогнуть стержень рукой и отпустить, после некоторых колебаний он вновь выпрямится (устойчива прямолинейная форма равновесия).
С увеличением нагрузки частота собственных колебаний уменьшается, и при критической нагрузке она равна нулю.
При достижении нагрузкой критического значения стержень слегка искривляется и касается одного из упоров. Если изогнутый стержень руками вернуть в исходное прямолинейное положение и отпустить, он вновь искривится, т.е. прямолинейная форма перестала быть устойчивой. - Снимаем отсчет по шкале осадки пружины δ и заносим его в журнал испытаний, разгружаем образец вращением маховика против часовой стрелки.
- Определяем по паспорту установки коэффициент жесткости пружины С.
- Вычисляем опытное значение критической силы
Fкр оп= С · δ. - Сравниваем величины Fкр оп и Fкр т, определяем процент расхождения и делаем соответствующие выводы.
Контрольные вопросы
- Какой изгиб называется продольным?
- Что понимается под критической силой?
- От чего зависит величина критической силы?
- Когда применима формула Эйлера?
- Что такое коэффициент приведения длины и чему он равен при различных случаях закрепления концов сжатых стержней?
- Как определяется критическое напряжение, если формула Эйлера неприменима?
- Чему равна гибкость стержня?
- Как определить предельную гибкость?
- Как опытным путем определить значение критической нагрузки?
Далее: