Пример решения задачи построения эпюры внутренних продольных сил Nz для стержня с продольно распределенной нагрузкой q.
Задача
Рассчитать значения внутренних продольных сил N и построить их эпюру для стержня к которому приложены сосредоточенная сила и продольная равномерно распределенная нагрузка
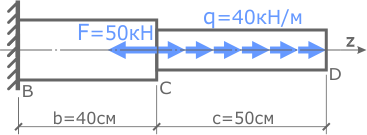
для дальнейшего расчета на прочность.
Другие примеры решений
Помощь с решением задач
Пример решения
Предыдущий пункт решения задачи: Расчет опорной реакции в заделке стержня.
Рассматриваемый стержень имеет два силовых участка, обозначим их цифрами I и II.
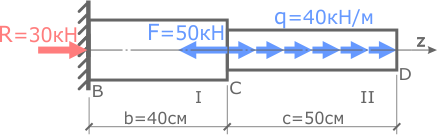
Для расчета внутренних сил на них воспользуемся методом сечений.
Начнем с первого силового участка BC.
Мысленно рассекаем участок в произвольном месте между сечениями B и C.
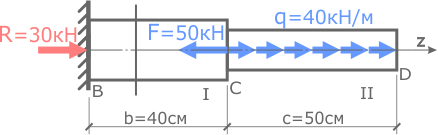
Выбираем для рассмотрения левую часть стержня, так как к ней приложено меньшее количество нагрузок.
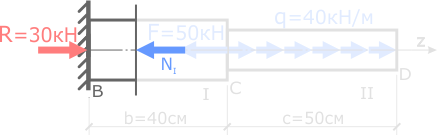
Внутренняя сила на I силовом участке равна сумме внешних сил (с учетом правила знаков при растяжении-сжатии) приложенных к рассматриваемой отсеченной части стержня:
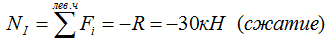
Так как на данном участке нет распределенной нагрузки, полученное значение NI будет одинаковым для всех сечений первого участка.
Переходим на второй силовой участок CD.
Проведя сечение,
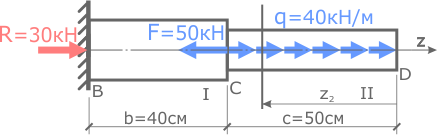
рассматриваем правую часть стержня.
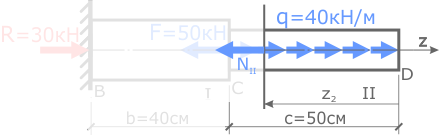
На данном участке есть распределенная нагрузка поэтому необходимо показать расстояние от границы участка до рассматриваемого сечения обозначив его переменной z2.
Интервал возможных значений переменной z2 лежит в пределах от 0 до 50см, т.е. 0 ≤ z2 ≤ 0,5м.
Выражение для расчета NII
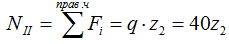
В полученном выражении переменная z2 в первой степени, следовательно, зависимость линейная.
Рассчитаем значения внутренней силы NII на границах участка при z2=0 и z2=0,5м.
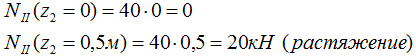
По полученным данным строим эпюру N.
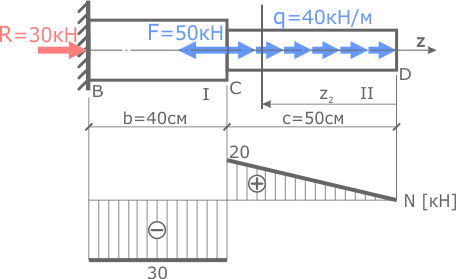
На I участке в соответствии с выбранным масштабом откладываем вниз от базовой линии значение 30 кН и проводим горизонтальную линию в пределах участка.
На II участке было получено 2 значения. Переменная z2 откладывалась от правой границы участка (сечения D) поэтому под сечением D где z2=0 ставим точку на базовой линии.
Под сечением C где z2=0,5м откладываем значение 20кН.
Полученные точки соединяем прямой линией, проставляем знаки, заштриховываем и проверяем построенную эпюру.