Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.
Посмотреть подробные примеры построения эпюр >>
Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.
Рассмотрим некоторые примеры на построение эпюр в балках:
Эпюры при чистом изгибе
Для консольной балки:
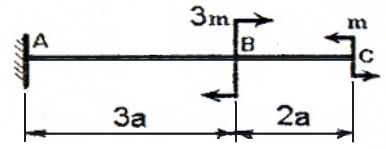
имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.
Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z1 ≥ 2a (рис. 2 а,г)
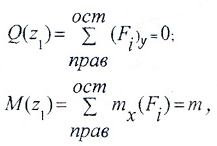
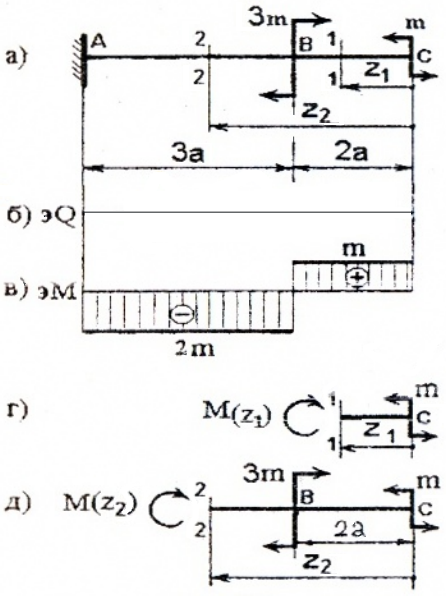
т.е. Q(z1)=0 на всем участке, а M(z1)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.
II силовой участок (AB): 2a ≥ z2 ≥ 5a (рис. 2 а,д)
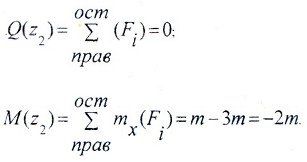
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).
Более нагруженным оказался участок AB, он и является опасным: Mmax=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.
Эпюры при поперечном изгибе
Построение эпюр Q и M для балки, изображенной на рис. 3
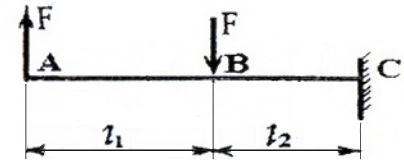
проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г)
Q(z1)= F=const, на всем участке постоянная величина,
M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам:
M(z1=0)=F×0=0 – в сечении A;
M(z1=l1)=F× l1 — в сечении B.
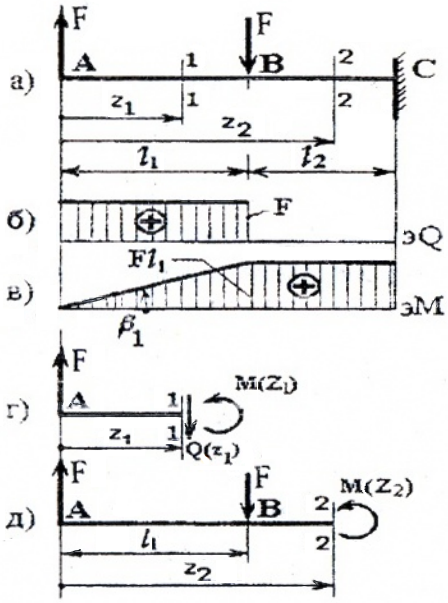
II силовой участок (BC): l1 ≥ z2 ≥ (l1+ l2) (рис. 4, а, д)
Q(z2)= F-F=0;
M(z2)=F×z2— F×(z2— l1)=F ×l1=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке — деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.
Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.
Геометрическая проверка эпюр
Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим:
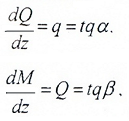
где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α1=0 (линия эпюры Q горизонтальна), следовательно,
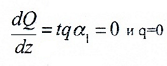
распределенная нагрузка отсутствует;
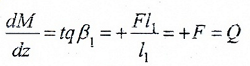
функция M (z1) – возрастающая.
На участке “BC”:
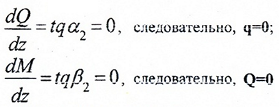
Так как все дифференциальные проверки выполняются, эпюры построены верно.
Эпюры для двухопорных балок
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),
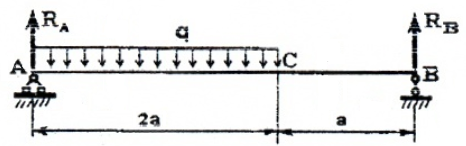
необходимо вначале найти опорные реакции и только потом строить эпюры.
Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.
Записываем уравнения и находим значения реакций:
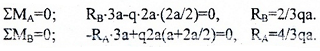
Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑FY=0 или ∑MС=0.
Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).
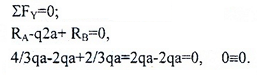
Для построения эпюр рассмотрим два силовых участка:
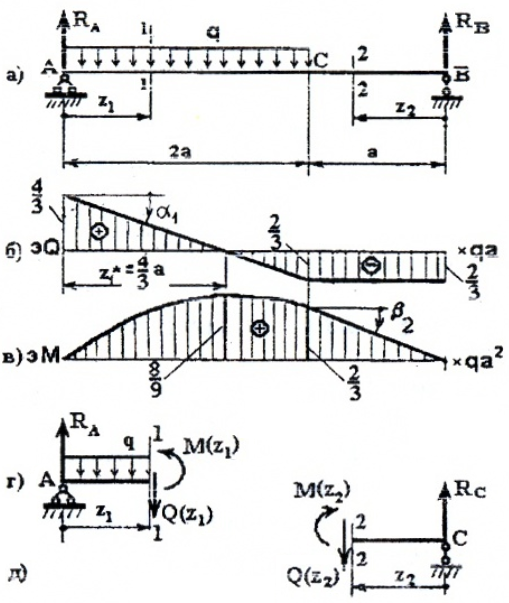
I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г)
Q(z1)=RA-qz1 — прямая, которую строим по двум граничным точкам:
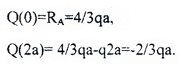
M(z1)=RAz1-qz1(z1/2)= RAz1-qz12/2 – парабола.
Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует Mmax(z*), и дифференциальной зависимости:
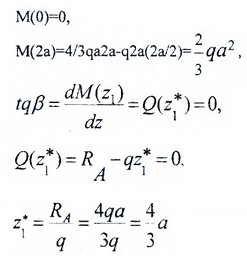
Определяем экстремум эпюры M на участке:
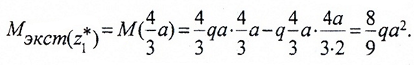
II участок (BC): 0 ≥ z2 ≥ a (рис. 6, а, д)
Q(z2)= -RB= -2/3qa;
M(z2)=RBz2,
M(z2=0)=0,
M(z2=a)=2/3qa2.
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z1 ≥ 2a
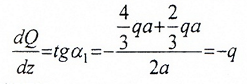
— направлена вниз, функция Q(z1) – убывающая.
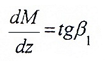
— проверка визуально: чем больше угол наклона β1, тем больше значение Q(z1).
II силовой участок: 0 ≥ z2 ≥ a.
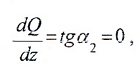
следовательно, q=0.
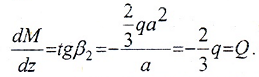
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z1*=4/3a
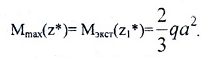
По силе в сечении «A»
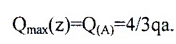
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.
Далее: