Пример решения задачи по расчёту многопролетной балки: кинематический анализ, определение реакций опор и построение эпюр внутренних поперечных сил и изгибающих моментов.
Многопролетной (шарнирной) балкой называется статически определимая система, состоящая из ряда однопролетных и консольных балок, соединенных между собой шарнирами.
В большинстве случаев на практике возведение многопролетных балок выгодно с точки зрения снижения расхода материалов.
Рассмотрим типовой пример расчета многопролетной статически определимой балки (рисунок 3.17):
Кинематический анализ
- W = 3×6 − 3×3 − 2×2 −5 = 0, следовательно система может быть неизменяемой;
- Структурный анализ: диск АВ вместе с диском "земля" образует единый диск, который соединен с диском СDЕGН с помощью трех непараллельных и непересекающихся в одной точке стержней.
Система в целом неизменяема.
Расчет реакций опор
После кинематического анализа выполняется определение опорных реакций и реакций связей.
Для этого: заменим внутренние (шарниры В и С) и внешние (заделка А, шарнирно-подвижные опоры D и G) связи их реакциями, которые будут представлять собой неизвестные пока сосредоточенные воздействия.
После этого разъединим заданную систему на элементы.
Рассматривая каждый элемент с учетом их совместной работы, определим опорные реакции и реакции связей.
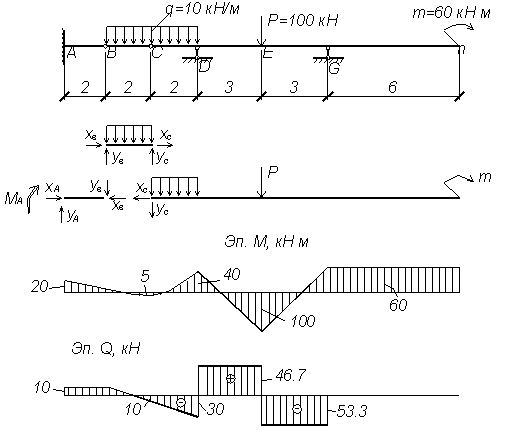
Рисунок 3.17 – Пример расчета многопролетной балки
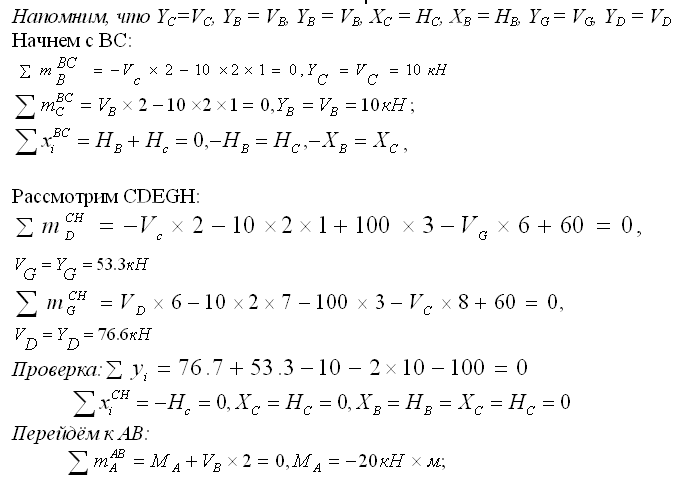
Построение эпюр
Построение эпюры изгибающих моментов
Для решения задачи методом сечений имеем шесть (AB, BC, CD, DE, EG, GH) силовых участков.
Участок AB:
Начало силового участка примем в сечении A:
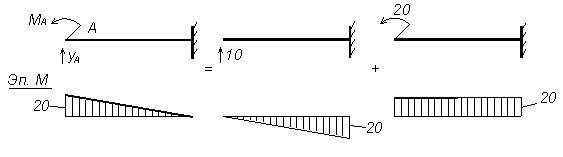
Рисунок 3.18 – Построение эпюры M на участке AB
Если же за начало силового участка принять сечение B (это приводится здесь для доказательства того, что выбор начала участка не влияет на окончательную эпюру):
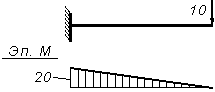
Рисунок 3.19 — Построение эпюры M на участке BA
Участок BC:
Начало консоли примем в точке B.
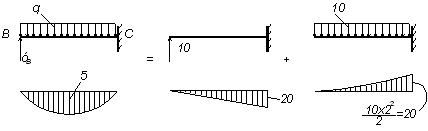
Рисунок 3.20 — Построение эпюры M на участке BC
Участок CD:
Начало участка в сечении C (очевидно, что сечение D пока началом участка быть не может).
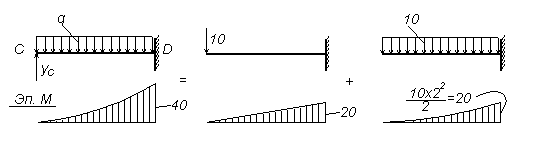
Рисунок 3.21 — Построение эпюры M на участке CD
Участок DE:
Начало силового участка примем в сечении D.
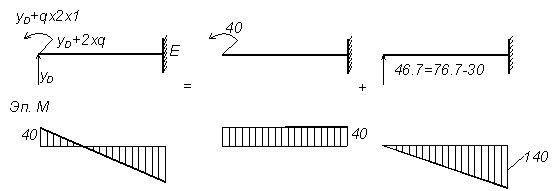
Рисунок 3.22 — Построение эпюры M на участке DE
Участок GH:
Начало силового участка примем в сечении «H».

Рисунок 3.23 — Построение эпюры M на участке GH
Участок EG:
Начало силового участка примем в сечении «G».
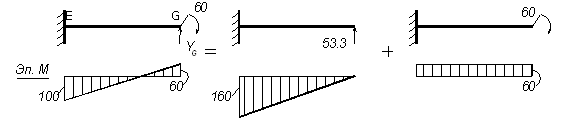
Рисунок 3.24 — Построение эпюры M на участке EG
Окончательно получим эпюру моментов, изображенную на рисунке 3.17.
Построение эпюры поперечных сил
Первоначально рассмотрим силовые участки с линейной эпюрой моментов.
Участок GH:
Эпюра моментов параллельна базису (оси участка), поэтому тангенс угла наклона эпюры моментов, а значит и поперечная сила на этом участке равны нулю.
Участки EG и DE:
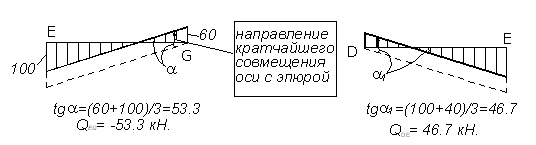
Участки AB и BC:
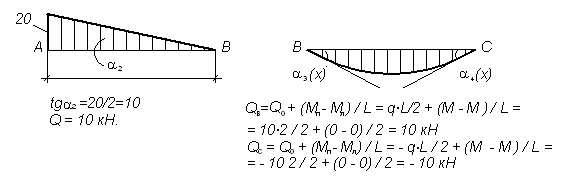
Участок CD:
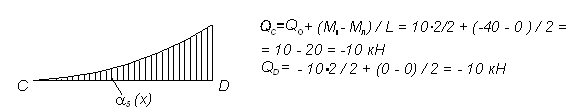
Рисунок 3.25 – Построение Эпюр Q на участках EG, DE, AB, BC, CD
Окончательная эпюра Q изображена на рисунке 3.17.
Построение эпюры продольных сил
Отсутствие горизонтальных составляющих всех реакций позволяет сделать вывод о том, что продольные усилия на всех силовых участках отсутствуют.
Общая статическая проверка.
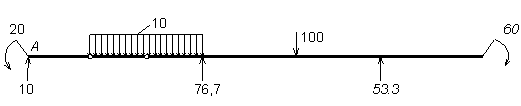
Рисунок 3.26 – Статическая проверка
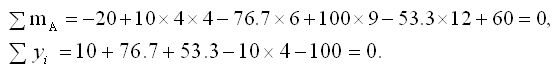
Далее: