Статически определимыми системами (СОС) называют стержневые, балочные конструкции и рамы, во всех элементах которых, для определения внешних и внутренних усилий (в том числе реакций связей) достаточно только уравнений равновесия.

Если же уравнений статики окажется недостаточно, то говорят, что мы имеем дело со статически неопределимыми системами (СНС).

Обычно под расчетом систем понимают оценку их несущей способности, прочности и жесткости.

Типы статически определимых систем

Расчетные схемы статически определимых систем имеют следующий вид:

Балки и рамы

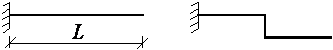
Рисунок 2.4 – Прямая и ломаная консоль

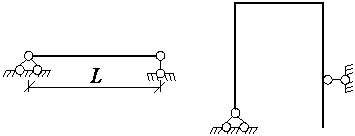
Рисунок 2.5 — Простая балка и рама

Трехшарнирные системы

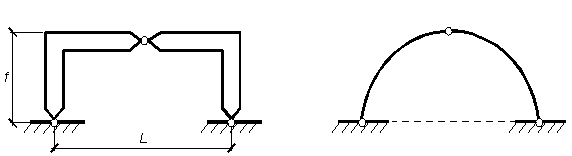
Рисунок 2.6 – Трехшарнирные рама и арка

Фермы

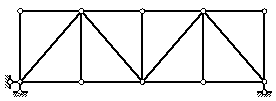
Рисунок 2.20 – Классическая ферма

Многопролетные системы (балки, рамы)

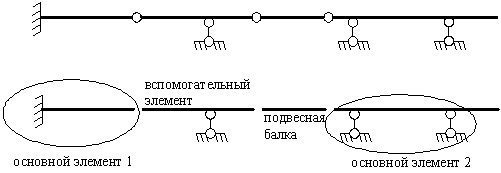
Рисунок 2.29 – Многопролетная балка

Аналитические способы расчета статически определимых систем

I этап. Определение опорных реакций

Опорные реакции для статически определимых систем определяются при помощи уравнений равновесия:

1. ∑Fx=0, ∑Fy=0, ∑m_k = 0
2. ∑m_k=0, ∑m_i=0, ∑Fx = 0 (∑Fy=0)
3. ∑m_k=0, ∑m_А=0, ∑m_В=0

Для трехшарнирных систем для определения опорных реакций необходимо составить 4 уравнения равновесия:

— для систем без затяжки

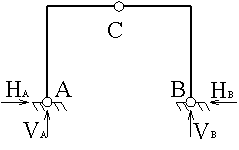
∑m_A = 0 => V_B

∑m_B= 0 => V_A

∑m_c^лев=0=>H_A ∑x =0

∑m_c^пр =0=> H_B

При отсутствии горизонтальной нагрузки Н_А = H_B=H.

— для систем с затяжкой

∑m_A = 0 => V_B

∑m_B = 0 => V_A

∑x = 0 => H_A

∑ М_с^лев = 0 (∑ М_с^пр = 0) => N_зат

Для многопролетных систем необходимо выделить основные, вспомогательные и подвесные элементы посредством построения поэтажной схемы (согласно рисунка 2.29).

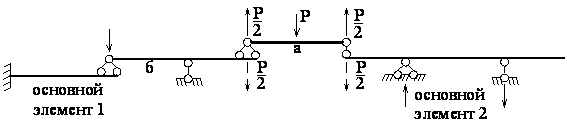
Рисунок 2.30 – Поэтажная схема для схемы рисунка 2.29

После построения поэтажной схемы расчет начинают вести с верхнего этажа.

Нижележащие этажи рассчитываются на приложенную внешнюю нагрузку и передаточное давление.

Передаточное давление равно опорным реакциям верхнего этажа взятого с обратным знаком.

Определение опорных реакций ведется обычным способом.

Опорные реакции в фермах находятся также как и в балках.

Варианты статически определимых систем

Рассмотрим основные варианты статически определимых систем, их расчетные схемы и соответствующие уравнения для определения опорных реакций:

Балка на двух опорах

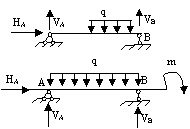
∑x=0

∑M_A=0

∑M_B=0

Консольная балка

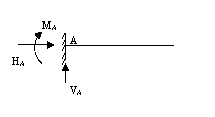
∑X=0

∑Y=0

∑M_A=0

Ломаные балки

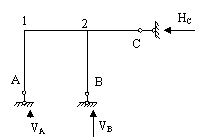
∑X=0

∑M₁=0

∑M₂=0

Трехшарнирные системы

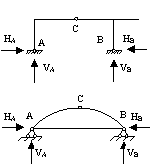
∑X=0

∑M_A=0

∑M_B=0

∑M_с^лев=0

(∑M_с^прав=0)

Фермы

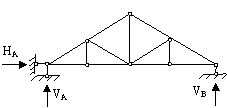
∑X=0

∑M_A=0

∑M_B=0

Многопролетные системы

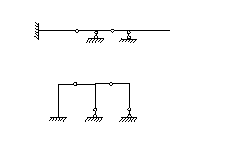
Для определения опорных реакций и внутренних усилий требуется построение поэтажной схемы.

II этап. Определение внутренних усилий

Определение внутренних усилий и построение их эпюр для простейших элементов рассматривается в курсе сопротивления материалов.

Отметим, что в курсе "Строительная механика" практически та же методика расчета, но используется она для более сложных систем.

Если мы мысленно отсечем часть некоторой произвольной балки, загруженной произвольной нагрузкой, то в сечении балки в общем случае возникнет комплекс внутренних усилий (рисунок 2.31):

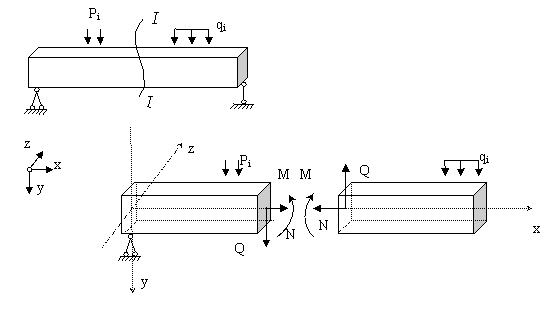
Рисунок 2.31 – Виды внутренних усилий, возникающих в сечении балки

Сформулируем определения внутренних усилий и правила знаков для них.

Изгибающий момент М в сечении I-I представляет собой сумму моментов всех внешних сил, приложенных к рассматриваемой части балки относительно оси OZ.

Момент считается положительным, если он вызывает растяжение нижних волокон рассматриваемой отсеченной части.

Поперечная сила Q — внутреннее усилие, равное по величине сумме проекций всех внешних сил, приложенных к рассматриваемой части балки на ось OY.

Поперечная сила считается положительной, если она вызывает вращение рассматриваемой отсеченной части по часовой стрелке.

Продольная сила N — внутреннее усилие, равное по величине сумме проекций всех внешних сил, приложенных к рассматриваемой части балки на ось ОХ.

Продольная сила считается положительной, если она вызывает растяжение рассматриваемой отсеченной части.

Далее: Эпюры внутренних усилий в балках

---

Теория и примеры решения задач по предметам: