Пример решения задачи по определению величины горизонтального движения корпуса двигателя заданной массы от сил, создаваемых кривошипом, вращающимся с постоянной угловой скоростью.

Задача

Горизонтальный поршневой двигатель установлен без крепления на горизонтальном гладком фундаменте (рисунок 13). Кривошип OA длиной r вращается с постоянной угловой скоростью ω.

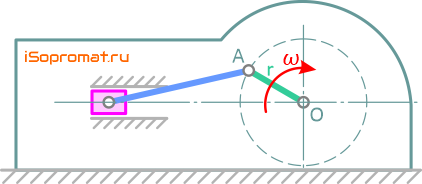
Рисунок 13

Принимая длину шатуна равной длине кривошипа, и считая, что массы движущихся частей приведены к двум массам m₁ и m₂, сосредоточенным в пальце кривошипа и в центре поршня, определить горизонтальное движение корпуса двигателя, если его масса равна m₃. В начальный момент поршень занимал крайнее левое положение, а система находилась в покое.

Теория по теме задачи

Решение

Рассмотрим двигатель как механическую систему, состоящую из трех масс m₁, m₂ и m₃. На нее действуют внешние силы: P₁, P₂, P₃ — силы тяжести; N — нормальная реакция гладкого фундамента.

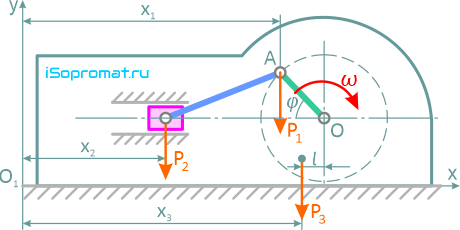
Рисунок 14

Поскольку требуется найти горизонтальное движение корпуса, воспользуемся первым уравнением (1.10′):

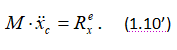
Пусть x₁, x₂, x₃ – абсциссы масс системы в текущий момент t. Тогда абсциссу центра масс системы можно записать в виде выражения

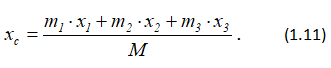
Выразив все абсциссы через искомую координату x₃, имеем

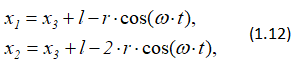
где l = const – разность абсцисс точки O и массы m₃.

Подставим эти абсциссы в формулу (1.11), получим

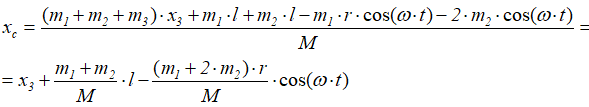
Дифференцируя x_c дважды по времени и подставляя в (1.10′), будем иметь дифференциальное уравнение движения центра масс корпуса двигателя:

В данной задаче R^e_x = 0, т.к. при выбранных осях все внешние силы параллельны оси O₁y. Уравнение (13) примет вид

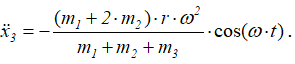
Интегрируя, найдем

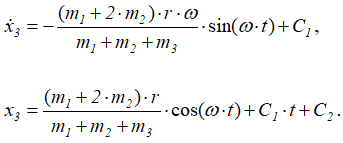
Учитывая начальные условия движения корпуса

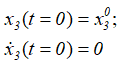
получим

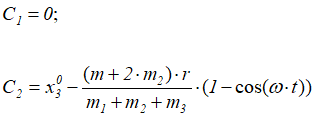
где x⁰₃ — начальная абсцисса корпуса двигателя.

Итак,

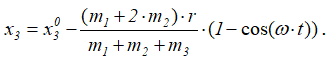
Это и есть уравнение движения корпуса двигателя. Таким образом, корпус двигателя будет совершать гармонические колебания с амплитудой

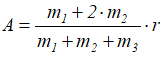
и круговой частотой ω.

---

Далее: