Пример решения задачи по определению с помощью принципа возможных перемещений, опорных реакций составной конструкции, находящейся в равновесии под действием распределенной нагрузки q, силы F и момента M.
Задача
С помощью принципа возможных перемещений определить реакцию опоры A составной конструкции, находящейся в равновесии под действием распределенной нагрузки интенсивности q, силы F и момента M.
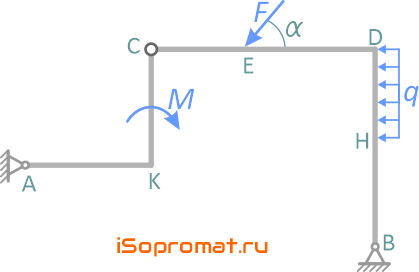
Геометрию и размеры конструкции считать известными.
Решение
Заменим распределенную нагрузку сосредоточенной силой Q = q∙DH. Эта сила приложена в середине отрезка DH – в точке L.
Силу F разложим на составляющие, спроецировав ее на оси: горизонтальную Fxcosα и вертикальную Fysinα.
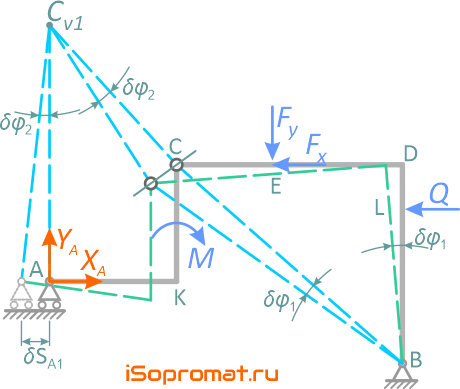
Чтобы решить задачу с помощью принципа возможных перемещений, необходимо, чтобы конструкция могла перемещаться и при этом чтобы в уравнении работ была одна неизвестная реакция. В опоре A реакция раскладывается на составляющие XA, YA.
Для определения XA изменим конструкцию опоры A так, чтобы точка A могла перемещаться только по горизонтали. Выразим перемещения точек конструкции через возможный поворот части CDB вокруг точки B на угол δφ1, часть AKC конструкции в этом случае поворачивается вокруг точки CV1 — мгновенного центра вращения (рисунок 2.5) на угол δφ2, и перемещения точек L и C – будут
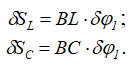
В то же время
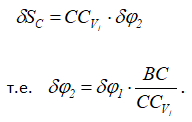
Уравнение работ удобнее составить через работу моментов заданных сил, относительно центров вращений.
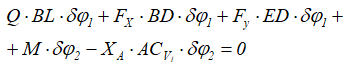
Реакция YA работу не совершает. Преобразуя это выражение, получим
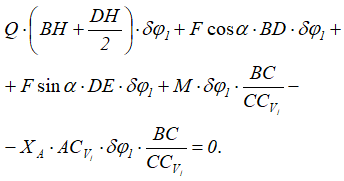
Сократив на δφ1, получим уравнение, из которого легко находится XA.
Для определения YA конструкцию опоры A изменим так, чтобы при перемещении точки A работу совершала только сила YA (рисунок 2.6). Примем за возможное перемещение части конструкции BDC поворот вокруг неподвижной точки B — δφ3.
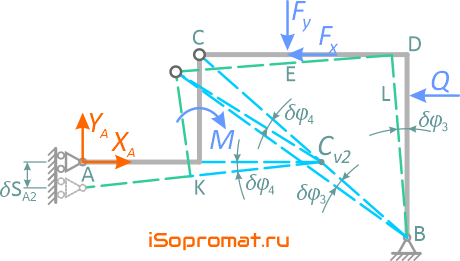
Для точки C
![]()
мгновенным центром вращения для части конструкции AKC будет точка CV2, и перемещение точки C выразится:
![]()
Приравнивая перемещения точки C для двух частей, получаем
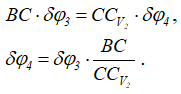
Составим уравнение работ:

Сократив на принятое возможное перемещение — δφ3, можно определить реакцию YA.
Полная реакция в точке A:
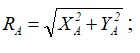
направление RA определяется углами:
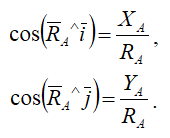
Далее: