Пример решения задачи по определению угловой скорости колеса заданного радиуса и приводимого в движение приложенным моментом из состояния покоя, которое посредством невесомой нити двигает груз по шероховатой поверхности.
Задача
Однородное колесо 1 массой M и радиусом r1 приводится в движении из состояния покоя приложенным моментом mвр. Груз 2 массой m посредством невесомой нити, намотанной на колесо барабана, движется по шероховатой поверхности, коэффициент трения скольжения которой равен f (рисунок 3.6).

Определить угловую скорость колеса в 4 случаях:
- а) mвр=A;
- б) mвр=a∙t, где a – постоянная, t – время;
- в) mвр=b∙φ, где b – постоянная, φ – угол поворота барабана;
- г)
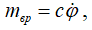
где c – постоянная,
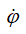 – угловая скорость колеса.
– угловая скорость колеса.
Пример решения
Механическая система состоит из двух тел: барабана 1, вращающегося вокруг оси x, и груза 2, движущегося поступательно.
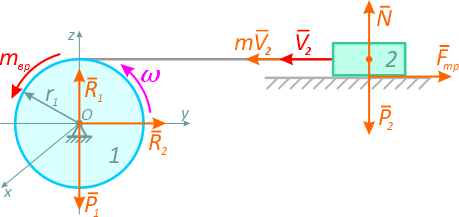
Выделим все силы, действующие на систему:
P1 = M∙g – сила тяжести барабана;
R1 и R2 – составляющие реакции колеса по осям Oz и Oy;
mвр – вращающий момент;
P2 = M∙g – сила тяжести груза;
N – нормальная реакция плоскости;
Fтр = f∙N = f∙m∙g – сила трения при скольжении груза о плоскость.
Согласно теореме об изменении момента количества движения механической системы относительно оси
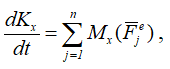
где
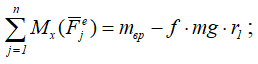
Kx – кинетический момент системы.
Кинетический момент системы определяется по формуле
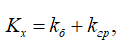
где kб – кинетический момент барабана;
kгр – кинетический момент груза;
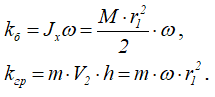
Тогда
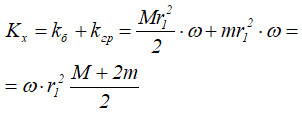
Итак,
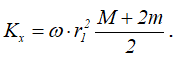
Окончательно получим
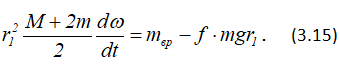
Решим последнее соотношение относительно угловой скорости колеса в четырех случаях, указанных в условии задачи.
Случай (а) mвр=A (A = const).
Для удобства в выражении (3.15) введем для момента инерции системы обозначение
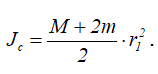
Тогда
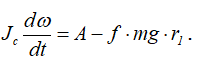
Разделив переменные и проинтегрировав обе части уравнения, получим
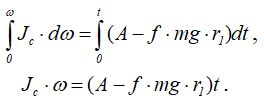
Окончательно будем иметь
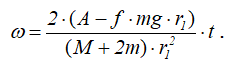
Случай (б) mвр = a∙t.
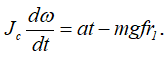
Разделив переменные и проинтегрировав обе части этого уравнения
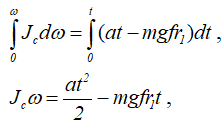
получим
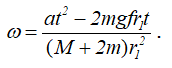
Случай (в) mвр = b∙φ.
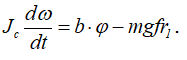
Так как правая часть зависит от угла поворота φ и прямого разделения переменных совершить невозможно, произведем замену переменной t:
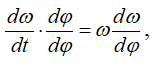
тогда
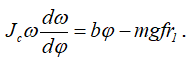
Разделим переменные и проинтегрируем полученное уравнение
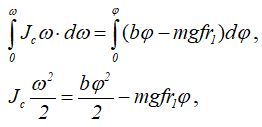
откуда
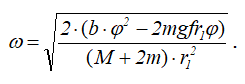
Случай (г)
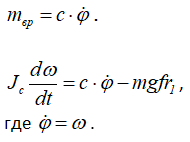
Разделив переменные, проинтегрируем и определим угловую скорость
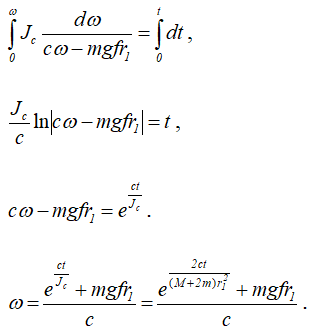
Далее: