Пример решения задачи по разделу динамика на определение угловой скорости вращающейся системы при заданном условии.

Задача

Стержень длиной 2l, вращается в горизонтальной плоскости вокруг неподвижной оси z (рисунок 3.7) с угловой скоростью ω.

По этому стержню, как по направляющей, могут скользить два одинаковых шара, радиусы которых пренебрежимо малы по сравнению с их расстоянием от оси вращения.

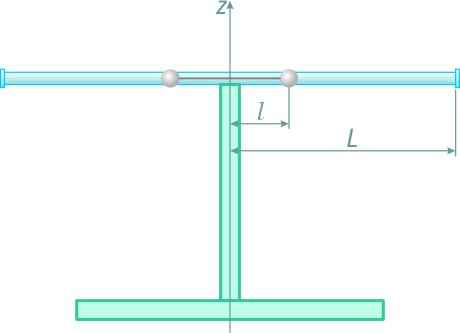
В начальный момент шары связаны нитью и находятся на расстоянии l от оси вращения.

Какова будет угловая скорость системы, если нить, связывающая шары, оборвется и расстояние каждого из шаров от оси вращения станет равным L?

Другие примеры решений >
Помощь с решением задач >

Пример решения

Для определения угловой скорости применим теорему о кинетическом моменте.

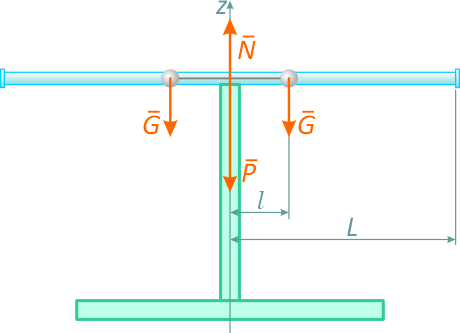
Так как внешними силами этой системы являются вес стержня P, вес шаров G и реакция оси вращения N, момент этих сил относительно оси z равен нулю, то на основании следствия 2 теоремы об изменении кинетического момента механической системы будем иметь

где K_z1 и K_z2 – кинетические моменты системы при первом и втором положениях шаров. Обозначая момент инерции стержня относительно оси z через J_z и принимая шары за материальные точки массой m=G/g, получаем

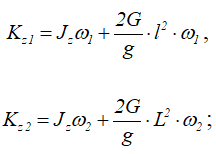
следовательно,

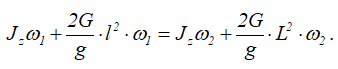
Отсюда

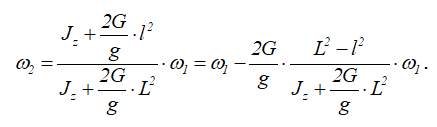
Таким образом, угловая скорость этой системы уменьшается под действием внутренних сил.

Другие примеры решения задач>