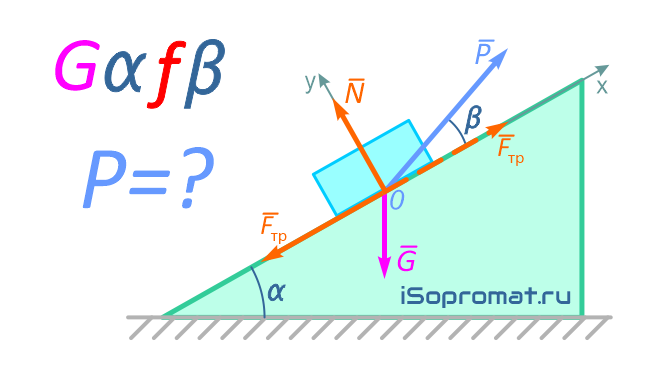
Пример решения задачи по определению величины силы, необходимой для удержания в равновесии тела в виде призматического бруска заданного веса на шероховатой наклонной поверхности с заданными углом наклона и коэффициентом трения.
Задача
Брусок весом G=100 Н удерживается в равновесии на шероховатой наклонной плоскости силой P, действующей под углом β=15°.
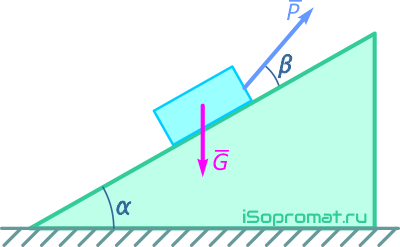
Угол наклона шероховатой поверхности α=45°, коэффициент трения между телом и поверхностью f=0,1.
Определить величину силы P, удерживающей в равновесии тело на шероховатой наклонной плоскости.
Решение
На тело действуют силы N, G, P и сила трения наклонной поверхности Fтр.
Возможны два случая предельного равновесия бруска и соответственно два предельных значения силы P и два направления (по наклонной плоскости вверх и вниз) силы трения в зависимости от направления возможного скольжения тела (вниз по наклонной плоскости или вверх).
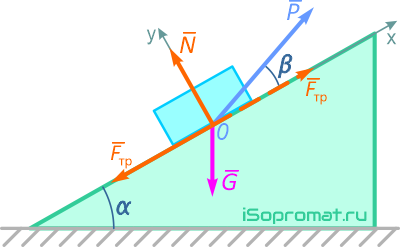
Составим уравнения равновесия призматического бруска в виде суммы проекций сил на координатные оси x и y (формулы 1.27 раздела 1.9):
B случае, когда тело скользит вверх
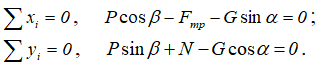
По закону Кулона
![]()
Решая уравнения относительно P, получаем
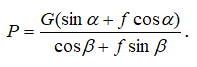
Подставляя числовые значения, имеем
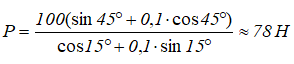
B случае, когда тело скользит вниз
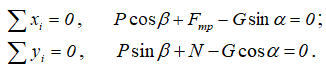
Решая эти уравнения относительно P, получаем
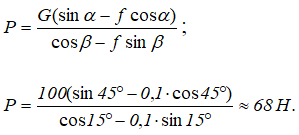
Таким образом, для силы P, удерживающей тело в равновесии имеем условие 68 ≤ P ≤ 78 Н.
Далее: