Рассмотрим общий порядок расчета внутренних силовых факторов в трехшарнирных системах.

Решение традиционно начинается с расчета реакций в опорах.

Определение реакций опор

При действии внешней нагрузки (сосредоточенных сил Р_i, и распределенных нагрузок q_i) на трехшарнирные системы, в каждой из опор возникают по две реакции: вертикальные — V_A (Y_A), V_B (Y_B) и горизонтальные (распор) – Н_A(X_A), Н_B(X_В) (рисунок 3.27).

Определение опорных реакций в таких системах производится с помощью составления уравнений равновесия.

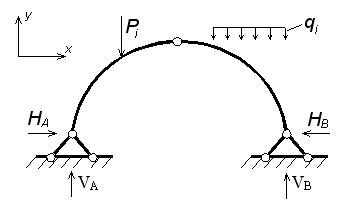
Рисунок 3.27 – Трехшарнирная арка

Наряду с тремя основными уравнениями статики для всей системы:

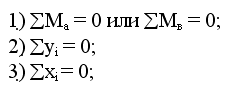
необходимо записать четвертое уравнение, выражающее условие равенства нулю изгибающего момента М_с в замковом шарнире «С»:

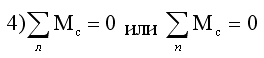
Определение опорных реакций таким способом довольно затруднительно, так как в ряде случаев приходится решать систему из четырех линейных уравнений.

При действии на трехшарнирную конструкцию только обычной вертикальной нагрузки, определение опорных реакций несколько упрощается.

Рассмотрим определение опорных реакций при действии только вертикальной нагрузки на примере трехшарнирной арки.

Арка с опорными шарнирами, расположенными на одном уровне

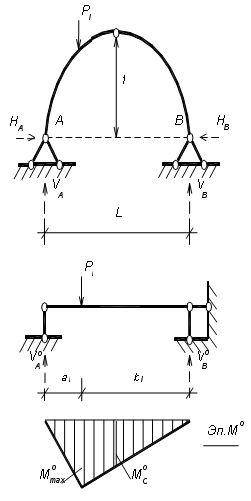
Рисунок 3.28 – Пример расчета трехшарнирной арки

Для определения опорных реакций V_A, V_B, Н_A, Н_B в арке составим упомянутые выше уравнения равновесия:

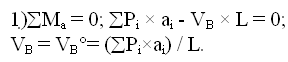
Получаем, что выражение для опорной реакции V_B в арке совпадает с аналогичным выражением в балке на двух шарнирных опорах того же пролета загруженной той же вертикальной нагрузкой.

Воспользуемся нулевым индексом для обозначения величин, характеризующих эту простую балку.

2) Опорную реакцию V_A можно определить из условия ∑Y_i= 0
или ∑М_B=0;

∑М_B= 0; V_A× L − ∑Р_i ×
b_i =0; V_A = (Р_i × b_i) / L = V_A^o

Делаем такой же вывод: определение V_B аналогично определению V_B°.

∑х_i = 0; Н_A− Н_B= 0; Н_A= Н_B = Н.

При действии лишь вертикальной нагрузки Р_i, горизонтальные опорные реакции (распор) равны между собой.

3) Для определения величины распора Н от действия внешней нагрузки составим четвертое уравнение:

Построим для приведенной схемы простой балки эпюру М, на которой величина момента под шарниром «С» равна:

М_c⁰=V_A× L/2 −∑Р_i × (L/2−a_i) − H×f = 0

Следовательно, последнее уравнение равновесия, выраженное через момент М, будет иметь вид: М_c⁰ −H×f = 0, H = М_c⁰/ f.

Таким образом: величина распора арки (рамы) при действии вертикальной нагрузки равна балочному моменту в сечении под замковым шарниром "С", уменьшенному в f раз.

Полученная формула справедлива при действии вертикальных сосредоточенных сил и распределенных нагрузок, как в арках, так и в трехшарнирных рамах.

Если трехшарнирная система имеет приподнятую затяжку, то претерпевает изменение только знаменатель:

H = М_c⁰/ (f-t),

где t — расстояние от оси затяжки до линии, соединяющей опорные шарниры (рисунок 3.29)

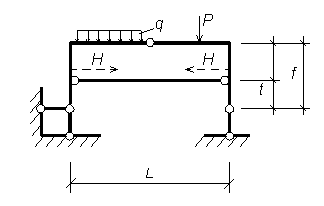
Рисунок 3.29 – Трехшарнирная рама с затяжкой

Расчет внутренних усилий

Определим величину и направление внутренних силовых факторов в трехшарнирной арке при действии вертикальной нагрузки

Для составления выражений внутренних усилий в трехшарнирной арке рассмотрим равновесие ее отсеченной части, расположенной слева от сечения.

а) Выражение для изгибающего момента М_к

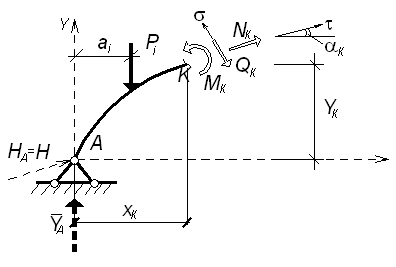
Рисунок 3.30 – Отсеченная левая часть арки

τ − ось, касательная к очертанию арки в точке «К»;

σ- ось, перпендикулярная к оси в точке «К»;

М, Q, N — внутренние усилия, направленные согласно соответствующим правилам знаков.

Составим уравнение равновесия для отсеченной части относительно точки «К»:

∑М_к = 0; V_A × x_к−∑ Р_i × (x_к − a_i) − H × y_к − М_к= 0.

Выделяя из этого уравнения М_к и учитывая, что:

V_A × x_к−∑ Р_i × (x_к − a_i) = М_к^o,

получим:

М_к= М_к^o − H × y_к

Анализируя это выражение можно заметить, что арочные системы рациональнее балочных, вследствие некоторого уменьшения величины балочного момента М за счет возникающего распора Н.

б) Выражение для поперечной силы Q_к

Для отсеченной части составим сумму проекций всех сил на ось:

∑ σ_i = 0: −Q_к + (V_A−∑ Р_i) × Соs α_к− Н × Sinα_к = 0;

Выделяя Q_к, с учетом того, что V_A − Р_i = Q_к^о, окончательно получим:

Q_к = Q_к^о × Соs α_к − Н × Sinα_к.

в) Выражение для продольной силы N_к

Для отсеченной части составим сумму проекций всех сил на ось:

∑ τ_i= N_к + Н × Соs α_к + (V_A−∑ Р_i) × Sinα_к= 0;

Выделяя N_к, с учетом того, что V_A − Р_i = Q_к^о, окончательно получим:

N_к = − Q_к^о × Sinα_к − Н × Соs α_к.

Рациональное очертание для трехшарнирной арки

Рациональным очертанием оси арки является такое, при котором момент в любом ее сечении равен нулю.

Так в предыдущем пункте, при действии вертикальной нагрузки, нами было получено следующее выражение для момента: М_к= М_к^o − H × y_к

Положив это выражение равным нулю и выделяя выражение для ординаты y_к, будем иметь:

y_к = М_к^o / Н = М_к^o × f / М_c^o

Анализ полученной формулы показывает:

− уравнение рациональной оси арки определяется видом нагрузки;

− при вертикальной нагрузке ось арки будет рациональной, если ее очертание меняется по закону изменения балочного момента.

Рассмотрим пример по определению рационального очертания арки, загруженной по длине равномерно распределенной нагрузкой.

Для произвольного сечения "К" с координатами y_к, x_к имеем: y_к = М_к^o / Н

Рассматривая равновесие по моментам левой отсеченной части, получим: М (x) = q × L × x/ 2 − q × x²/ 2

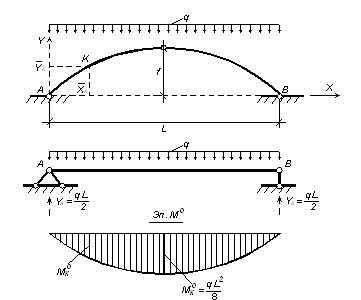
Рисунок 3.31 – Определение рационального очертания оси арки

Таким образом, рациональной осью для арки, загруженной равномерно распределенной нагрузкой по всему пролету является квадратная парабола.

Это объясняется тем, что постоянная нагрузка на арку и ее собственный вес составляют большую долю от общей нагрузки.

Как известно, эти виды нагрузок близки к равномерно распределенным.