Принцип Даламбера для механической системы гласит: для движущейся механической системы в любой момент времени геометрическая сумма главных векторов внешних сил, реакций связей, сил инерции равна нулю и геометрическая сумма главных моментов от внешних сил, реакций связей, сил инерции равна нулю.
Другими словами, все внешние силы действующие на механическую систему, при её движении всегда уравновешиваются силами инерции.
Для механической системы, состоящей из n точек, можно написать n уравнений вида
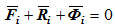
Сложив все эти уравнения и введя обозначения
ΣFi= FE — главный вектор внешних сил,
ΣRi= R — главный вектор реакций связей,
Фi= Ф — главный вектор сил инерции,
получим,
т.е.
Условием равновесия твердого тела является равенство нулю главного вектора и главного момента действующих сил.
С учетом этого положения и теоремы Вариньона (о моменте равнодействующей) получаем соотношение
примем обозначения:
Σri × Ri = M0R — главный момент реакций связей;
Σri × Фi = M0Ф — главный момент сил инерции.
Получим
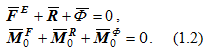
Формулы (1.1) и (1.2) выражают принцип Даламбера для механической системы.
Для движущейся механической системы в любой момент времени геометрическая сумма главных векторов внешних сил, реакций связей, сил инерции равна нулю и геометрическая сумма главных моментов от внешних сил, реакций связей, сил инерции равна нулю.
Полученные формулы представляют собой дифференциальные уравнения второго порядка, поскольку в каждом из них в силах инерции присутствует ускорение – вторая производная от закона движения точки.
Принцип Даламбера позволяет задачи динамики решать методами статики. Для механической системы могут быть написаны уравнения движения в форме уравнений равновесия, из которых могут быть определены неизвестные силы, в том числе и реакции связей (первая задача динамики).
Примеры решения задач >
Приведение сил инерции к центру масс >
