Пример решения задачи по определению перемещения тела при заданном перемещении груза механической системы тел, соединенных невесомыми и нерастяжимыми нитями через невесомые блоки.

Задача

Механическая система состоит из призмы 1 массой M₁, тел 2 и 3 массами M₂ и M₃ соответственно, соединенными невесомыми, нерастяжимыми нитями, переброшенными через невесомые блоки 4 и 5 (рисунок 11).

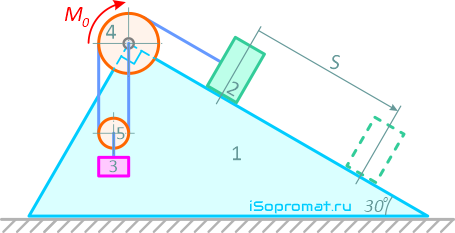
Рисунок 11

На систему действует постоянный момент, приложенный к блоку 4.

Требуется определить горизонтальное перемещение Δ призмы, скользящей по гладкой горизонтальной поверхности при заданном перемещении S груза 2 по поверхности тела. В начальный момент система находилась в покое.

Теория по теме задачи

Решение

Примем начало координат в левом конце призмы 1, тогда координаты, определяющие положение тел 1, 2, 3: x₁, x₂, x₃ соответственно.

Внешние силы, действующие на механическую систему: P₁, P₂, P₃, N, M₀, где P₁, P₂, P₃ – веса соответствующих тел; N – реакция связи гладкой поверхности.

Для решения задачи воспользуемся теоремой о движении центра масс

а в проекции на горизонтальную ось:

в данной задаче R^e_x = 0.

Так как в начальный момент система покоилась, то

следовательно, x_c = const.

Вычислим абсциссу центра масс системы в двух случаях:

1. для начального положения груза 2 (рисунок 12, а);
2. для положения системы, когда груз переместится по наклонной плоскости на расстояние, равное S (рисунок 12, б), а тело 1 предположительно переместится влево по горизонтали.

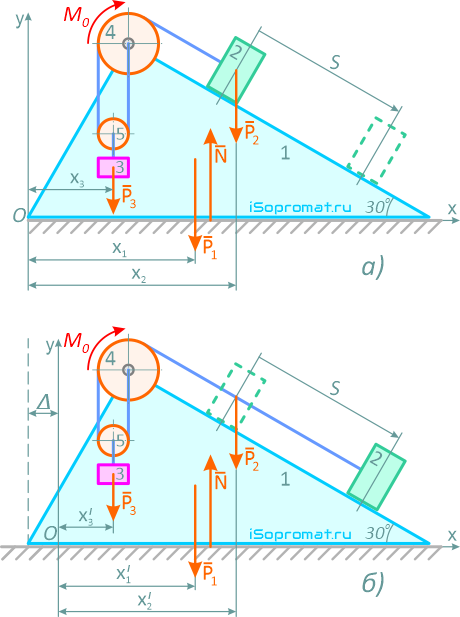
Рисунок 12

Абсцисса центра масс системы до перемещения груза 2 (рисунок 12, б)

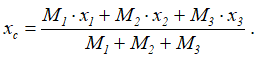
Обозначим перемещение тела Δ. После того как груз 2 переместился на расстояние S, призма со всеми телами системы, находящимися на ее поверхности, переместится влево на расстояние Δ, координаты центров тяжести тел по оси x (в системе xOy) будут следующими:

• для тела 1:
  
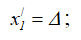
• для груза 2:
  

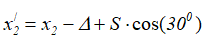
за счет переносного движения вместе с подвижной системой, связанной с телом 1, абсцисса x₂ уменьшилась на величину Δ, за счет переносного движения по поверхности призмы абсцисса увеличилась на расстояние S×cos30° — рисунок 13.

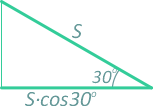
Рисунок 13

Груз 3 поднимется по вертикали вверх за счет того, что левая нить уменьшится на величину S. Абсцисса центра тяжести груза 3 за счет его переносного движения вместе с телом уменьшится на Δ и станет равной для груза 3:

Абсцисса центра масс системы после перемещения груза 2 по поверхности призмы

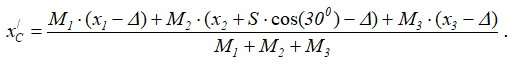
Приравнивая значения этих абсцисс, т.к. x_c = const, получим

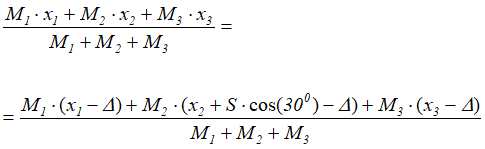
Упрощая, запишем

Знак «+» в результате говорит о правильности предположения, что призма сместится влево.

Таким образом, тело переместится влево на расстояние

---

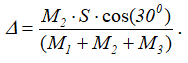
Далее: