Пример решения задачи на построение эпюры касательных напряжений τ для двутаврового сечения стальной балки.
Предыдущий пункт решения:
Построение эпюры нормальных напряжений.
Задача
Построить эпюру касательных напряжений для двутавра при следующих данных:
- Величина поперечной силы в сечении балки — 58,3 кН
- Двутавровое сечение — №24а
Другие примеры решений >
Помощь с решением задач >
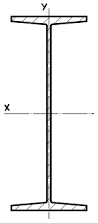
Пример решения
Расчет касательных напряжений в сечении балки ведется по формуле Журавского
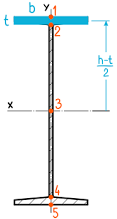
Двутавровое сечение по высоте имеет 5 характерных точек: крайние, среднюю и точки, на уровне которых стенка двутавра соединяется с полками.
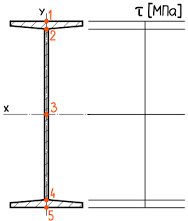
Обозначим их цифрами и проведем из них горизонтальные линии.
Начнем с крайних точек.
Статический момент в формуле Журавского одним из множителей включает в себя площадь сечения расположенную за рассматриваемой точкой.
Выше точки 1 и ниже точки 5 площадь сечения равна нулю, поэтому касательных напряжений там нет.
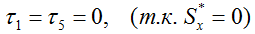
Максимальные напряжения следует ожидать в точке 3, потому что относительно нее будет самый большой статический момент. Его принимаем из сортамента.
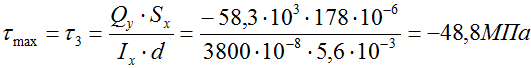
Чтобы найти напряжения в точках 2 и 4 надо сначала рассчитать статический момент полки двутавра.
Для этого временно заменим её прямоугольником со сторонами b и t, центр тяжести которого, очевидно будет на расстоянии t/2 от точки 1.
Это сильно упрощает расчеты без особого ущерба для правильности вычислений.
Статический момент полки определяется произведением её площади на расстояние от оси x до её центра тяжести.
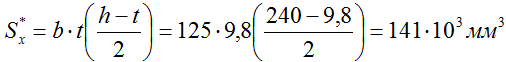
В этих точках сечение резко меняет свою ширину, поэтому получится скачок напряжений, и нам потребуется найти их величину в стенке и полке.
Начнем с полки, то есть сразу выше точки 2. Для этого в знаменатель формулы Журавского подставляем ширину полки b.
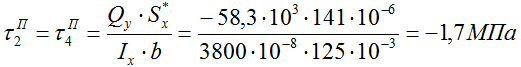
При расчете напряжения под точкой 2 подставляем толщину стенки d.
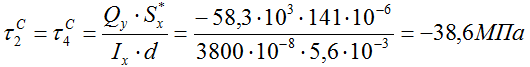
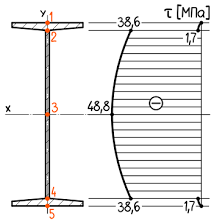
По полученным значениям строим эпюру касательных напряжений
