Пример решения задачи на построение эпюры нормальных напряжений σ для двутаврового сечения стальной балки.
Задача
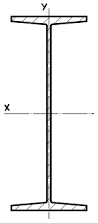
Построить эпюру нормальных напряжений σ для двутавровой балки при следующих данных:
- Изгибающий момент в сечении балки — 45 кН
- Двутавровое сечение балки — №24а
Пример решения
Построим эпюру нормальных напряжений для двутаврового сечения балки при ее поперечном изгибе.
Эпюру σ будем строить для сечения балки в точке C, где величина изгибающего момента составляет 45 кНм. В этом месте сжимаются нижние слои балки (т.к. в рассматриваемом сечении знак изгибающего момента отрицательный).
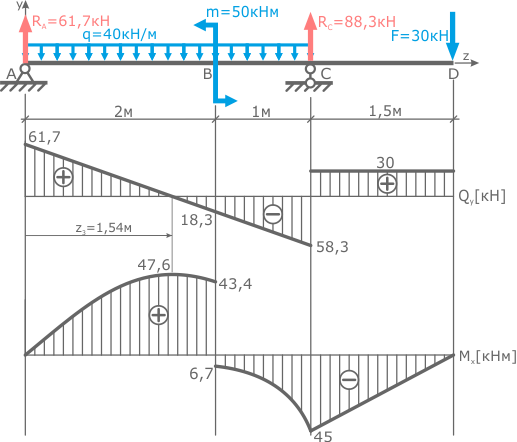
В предыдущем пункте решения задачи для балки по условию прочности был выбран двутавр под номером 24а, для которого из соответствующего сортамента прокатной стали выпишем следующие данные:
- Осевой момент инерции сечения: Ix=3800 см4,
- Высота сечения: h=240 мм,
- Толщина полки (горизонтальной части двутавра): t=9,8 мм.
Нормальные напряжения σ в произвольной точке поперечного сечения балки рассчитываются по формуле
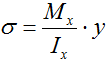
где
Mx – величина изгибающего момента в соответствующем сечении,
Ix – момент инерции сечения относительно оси x,
y – расстояние от оси x до рассматриваемой точки поперечного сечения балки.
Mx и Ix для всех точек сечения одинаковы, следовательно изменение величины нормальных напряжений зависит от положения точки сечения.
Переменная y имеет первую степень, т.е. зависимость линейная, поэтому для построения эпюры достаточно найти значения σ в двух точках.
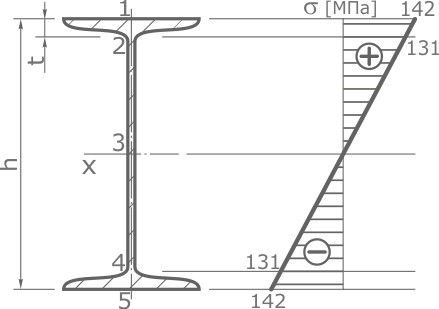
Двутавровое сечение имеет пять характерных точек:
Крайняя верхняя и нижняя точки (1 и 5 соответственно), центральная точка (3) и точки 2 и 4, где стенка переходит в полку.
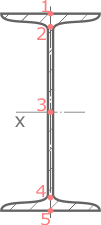
На оси x координата y=0, следовательно, нормальные напряжения в точке 3 отсутствуют
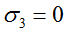
Наибольшая величина нормальных напряжений будет на максимальном удалении от центра сечения, в точках 1 и 5.
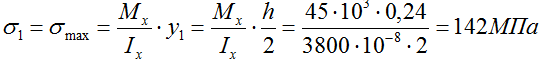
В указанном сечении балки сжимаются нижние слои, следовательно, верхние растягиваются. Поэтому в верхней точке 1 напряжения положительны (растягивающие) соответственно в точке 5 напряжения отрицательны (сжимающие), т.е.:
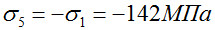
Так как сечение симметрично относительно оси x напряжения в т. 1 и 5 будут равны по величине, но противоположны по знаку.
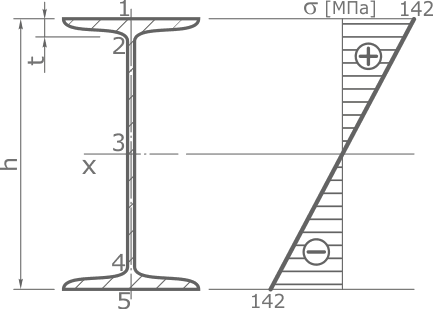
Отложив полученные значения, соединим их прямой линией.
Как видно, максимальные напряжения не превышают допустимых значений, что говорит о том, что выбранный номер двутавра обеспечивает необходимую прочность балки.
В дальнейшем, при проверке сечения на прочность, нам потребуются значения нормальных напряжений в точках 2 и 4. Рассчитаем их:
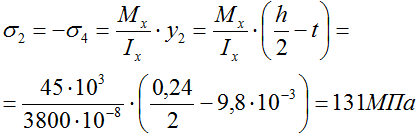
Далее: