Пример решения задачи по определению закона движения точки твердого тела массой m, начинающего скользить из состояния покоя по наклонной плоскости с заданным углом и коэффициентом трения скольжения f.
Задача
По наклонной плоскости из состояния покоя начинает скользить тело массой m = 1 кг (рисунок 5.1). Коэффициент трения скольжения f = 0,1.
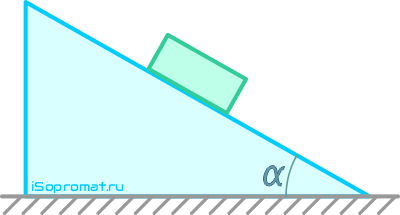
Определить закон движения точки, если угол α = 30°.
Решение
В данном случае тело движется поступательно, следовательно, его можно рассматривать как материальную точку. Направим ось x вдоль движения. Начало оси возьмем в начальном положении точки. Тогда x0= 0.
Поскольку движение начинается из состояния покоя, начальная скорость V0 тоже равна нулю.
Расположим тело в произвольный момент времени и покажем все силы, действующие на него, включая реакции связей. На тело действуют сила тяжести G, сила трения Fтр и нормальная реакция наклонной плоскости N (рисунок 5.2).
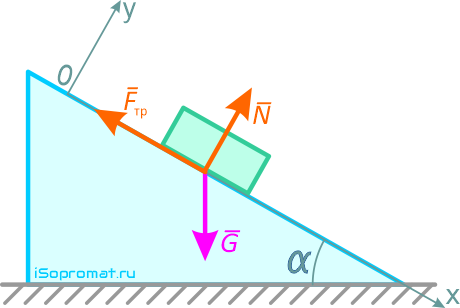
Запишем уравнение второго закона динамики в векторном виде
![]()
и в проекциях на оси координат
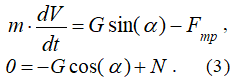
Из второго уравнения системы (3) можно определить величину нормальной реакции поверхности:
![]()
Первое уравнение системы (3) разделим слева и справа на m:
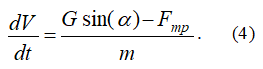
С точки зрения математики полученное уравнение является простейшим дифференциальным уравнением с разделяющимися переменными. Уравнение связывает две переменные величины – скорость точки и время.
Смысл разделения переменных заключается в том, чтобы все слагаемые уравнения, куда входит скорость, были с одной стороны от знака равенства, а слагаемые, куда входит время – с другой стороны знака равенства.
Умножив уравнение (4) на dt слева и справа, получим
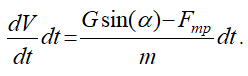
Сокращая слева на dt, получим:
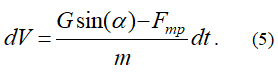
Величина
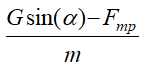
постоянная и ее можно внести под знак дифференциала. Тогда уравнение (5) перепишется в виде равенства двух дифференциалов:
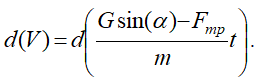
Если дифференциалы равны, то интегралы равны с точностью до постоянной величины:
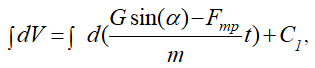
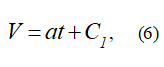
где
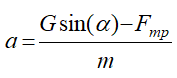
это ускорение точки.
Полученный результат дает зависимость проекции скорости на ось x от времени и от постоянной интегрирования C1.
Для определения постоянной C1 воспользуемся начальным значением скорости. Зная значение скорости точки в начальный момент времени V0, и подставляя его в (6), получим
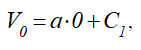
или C1 = V0.
Таким образом, зависимость скорости от времени примет вид
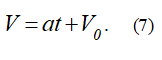
Учитывая, что
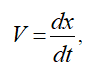
снова получим дифференциальное уравнение первого порядка относительно координаты x
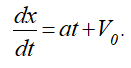
Снова разделим переменные
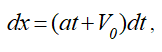
и после интегрирования получим
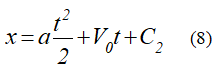
где C2 – вторая постоянная интегрирования. Для определения C2 воспользуемся значением координаты x в начальный момент. Получим C2 = x0.
Тогда (8) запишется в виде
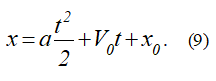
Подставляя начальные значения и исходные данные, получим
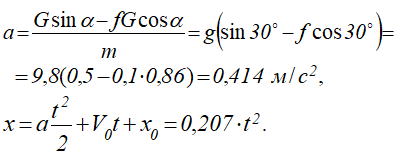
Ответ: Таким образом, тело движется вниз по наклонной плоскости по закону x = 0,207∙t2.
Далее: