Лабораторная работа №9. Экспериментальное определение перемещений при плоском поперечном изгибе двухопорной балки.
Цель работы – определить опытным путем прогибы и углы поворота сечений балки и сравнить их с теоретическими значениями.
Основные сведения
Под действием внешних нагрузок, расположенных в одной из главных плоскостей балки, ось балки искривляется в той же плоскости, в результате чего центры тяжести поперечных сечений перемещаются в направлении, перпендикулярном первоначальному (недеформированному) положению.
Согласно принятым допущениям в теории плоского изгиба деформация балки характеризуется двумя параметрами: вертикальным прогибом y и углом поворота θ. Угловые и линейные перемещения определяются аналитически путем интегрирования дифференциального уравнения изогнутой оси балки:
где EI – изгибная жесткость балки;
М – изгибающий момент в поперечном сечении балки;
у» – кривизна в рассматриваемом сечении балки (у – прогиб или вертикальные перемещения точек оси балки).
Могут использоваться и другие методы: универсальные уравнения метода начальных параметров, энергетические методы (интеграл Мора, способ Верещагина) и др.
Для опытного определения линейных и угловых перемещений используется настольная установка – двухопорная балка типа СМ-4 (рис. 9.1). Установка представляет собой балку, изготовленную из стальной полосы 7х40 мм, опирающуюся на две шарнирные опоры.
Конструкция установки позволяет изменять длину пролета, точку приложения нагрузки и ее величину, а также получать двухопорную консольную балку. Нагружение исследуемого образца осуществляется с помощью гиревого подвеса и набора грузов. Нагрузка прикладывается сосредоточенно.
Измерение прогибов и углов поворота опорных сечений балки производится с помощью индикаторов линейных перемещений часового типа с ценой деления 0,01 мм.
Для измерения угла поворота опорных сечений в конструкции шарнирной опоры установки предусмотрен рычаг (стержень) длиной lс = 150 мм, закрепленный перпендикулярно к оси балки и поворачивающийся вместе с сечением балки в результате ее деформации.
При этом свободный конец рычага описывает дугу (радиуса l0), длину которой и замеряет индикатор линейных перемещений, закрепленный на стойке опорного устройства и упирающийся штифтом в свободный конец рычага.
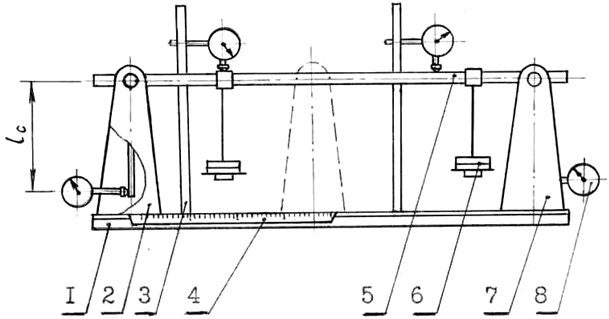
Рис. 9.1. Установка для определения перемещений при изгибе:
1 – основание; 2 – подвижная стойка; 3 – стержень;
4 – шкала перемещения подвижной стойки;
5 – исследуемый образец, 6 – гиревая подвеска с набором грузов; 7 – неподвижная стойка; 8 – индикатор
Порядок выполнения и обработка результатов
Определение величины прогибов и углов поворота спорных сечений производится в следующей последовательности.
Установка заранее подготавливается лаборантом (рис. 9.2,б) для выполнения на ней опыта по заданной схеме погружения балки (рис. 9.2.а).
Для заданной расчетной схемы в сечениях установки индикаторов производим подсчет перемещении любым из известных методов (т.е. находим два вертикальных перемещения у1Т и у2Т и два угловых перемещения в опорах θСТ, θKТ). Расчеты линейных и угловых перемещений могут быть выполнены на ЭВМ.
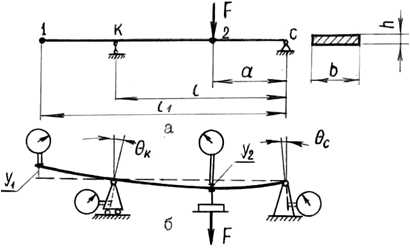
Рис. 9.2. Схема к определению перемещений
Затем приступаем к опытному определению этих же перемещений, для чего снимаем начальные показания со всех индикаторов и данные записываем в журнал.
Устанавливаем на гиревой подвес гирю весом, соответствующим заданной нагрузке F (например, 10 Н), и снимаем новые показания со всех индикаторов, записав их в журнал и подсчитав приращения.
Последовательно догружаем балку 2-3 раза дополнительными гирями того же веса, при этом общая нагрузка на гиревой подвес не должна превышать 60 Н.
После каждого нагружения записываем в журнал наблюдений показания индикаторов и подсчитываем приращения.
По окончании опыта балку разгружаем и сравниваем показания индикаторов с первоначальным.
Для подсчета опытных значений вертикальных перемещений в сечениях 1 и 2 балки подсчитываем средние арифметические приращения по каждому индикатору, замеряющему вертикальные перемещения — ΔПСР, которые и будут соответственно у1ОП = ΔП1СР и у2ОП = ΔП2СР в единицах измерения шкалы индикаторов.
Величина углов поворота определяется по формуле
где ΔПiСР – средние арифметические приращения отсчетов индикаторов, измеряющих длину дуги поворотов опорных сечений;
lС = 150 мм – расчетная длина рычага (радиус дуги).
Сравнение опытных результатов с теоретическими производим по формулам
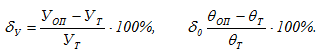
Полученные данные заносятся в журнал и делаются соответствующие выводы.
Контрольные вопросы
- Какими параметрами характеризуется деформация изгиба?
- Для чего нужно знать величины прогибов и углов поворота сечений?
- Что такое упругая линия балки? Как выглядит дифференциальное уравнение этой линии? Какие приняты при этом допущения?
- Какие теоретические способы определения перемещений в балках вам известны? Перечислите их, укажите достоинства и недостатки их применения.
- Перечислите, какие условные правила необходимо выполнять при использовании универсального уравнения упругой линии.
- Чем подтверждается пропорциональность между прогибами балки и нагрузкой на нее?
Далее: