Лабораторная работа №11. Экспериментальное определение величины опорной реакции в статически неопределимой балке.

Цель работы – определить опытным путем лишнюю опорную реакцию однажды статически неопределимой балки при ее изгибе и сравнить полученный результат с теоретическим.

Основные сведения

Система называется статически определимой, если внутренние усилия в ее элементах и реакции связей можно определить из условий равновесия статики. Система называется геометрически неизменяемой, если взаимные перемещения точек системы возможны лишь за счет деформации ее элементов.

То число внешних связей, при котором достигается геометрическая неизменяемость системы, называется необходимым числом связей. Всякую связь, наложенную сверх необходимой, называют дополнительной.

Наложение дополнительных связей на статически определимую систему увеличивает ее жесткость и прочность, но превращает ее в статически неопределимую систему, в которой реакции опорных связей и внутренние силовые факторы не могут быть определены с помощью уравнений равновесия статики. Степень статической неопределимости соответствует числу дополнительных связей.

Известно несколько методов расчета статически неопределимых систем. Наиболее простой и универсальный из них – метод сил, который заключается в следующем: устанавливается степень статической неопределимости системы, отбрасываются дополнительные связи, их действие заменяется неизвестными реакциями и записываются условия равенства нулю перемещений по направлению отброшенных связей.

Эти уравнения называются уравнениями совместности деформаций или каноническими уравнениями метода сил. Коэффициенты канонических уравнений, представляющие собой линейные или угловые перемещения, обычно определяются энергетическими методами.

Совместное решение уравнений статики и уравнений совместности деформаций дает возможность определить реакции всех связей.

При решении статически неопределимых задач вводятся следующие понятия: заданная система, основная система.

Основной системой называется любой из статически определимых (геометрически неизменяемых) вариантов рассматриваемой системы, полученный путем освобождения ее от лишних связей.

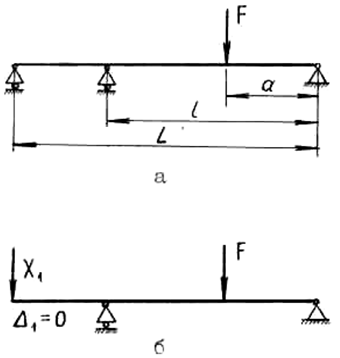
Рассмотрим вопрос определения лишней неизвестной для следующей заданной статически неопределимой системы (рис. 11.1, a). Эта схема может быть осуществлена на настольной установке двухопорной балки СМ-4 (описание см. в лаб. работе №9).

Для иллюстрации определения лишней неизвестной в однажды статически неопределимой системе заданную систему (рис. 11.1, а) выбираем такой, чтобы один из вариантов основной системы (см. рис. 11.1, б) представлял собой, двухопорную балку с консолью, соответствующую расчетной схеме, рассмотренной в лабораторной работе №9.

Порядок выполнения и обработка результатов

Порядок проведения испытаний следующий:

1. устанавливаем гиревые подвесы на конце консоли и в сечении приложения нагрузки F, при этом индикатор перемещений устанавливаем на конце консоли, (рис. 11 2, а);
2. снимаем начальный отсчет с индикатора П₁;
3. прикладываем заданную нагрузку F (опустить гирю весом, равным F) на гиревой подвес, расположенный в заданном по расчетной схеме сечении (см. рис. 11.2, б);
4. на индикаторе перемещений снимаем отсчет П₂. Разница отсчетов ΔП = П₂ – П₁ показывает величину перемещения консоли в двухопорной балке (основной системе);
5. чтобы основная система соответствовала заданной (т.е. стала эквивалентной заданной), необходимо на гиревой подвес, закрепленный на консоли, приложить нагрузку Х₁ такой величины, чтобы перемещение конца консоли стало равным нулю (из набора разновесов последовательно догружать гиревой подвес до тех пор, пока отсчет на индикаторе на положения П₂ вернется к значению П₁, т.е. ΔП = Δ₁ = 0 (см. рис. 11.2, в));
6. при этом величина X₁ (общий вес разновесов на гиревом подвесе консоли) будет соответствовать реакции дополнительной связи в заданной статически неопределимой системе;
7. опытное значение реакции Х₁ сравниваем со значением, полученным теоретическим расчетом (например, с помощью канонического уравнения метода сил), определив процент отклонения Х_оп от Х_Т, полученные значения заносим в журнал наблюдений.

Теоретические значения неизвестных реакций могут быть определены с помощью ЭВМ по программе, составленной кафедрой для выполнения лабораторных работ № 9,10,11.

Для этого необходимо на ЭВМ вызвать программу «LAB9.EXE», Программа работает в диалоговом режиме. После ввода всей необходимой исходной информации (c системе СИ) машина осуществляет расчет и выдает на экран дисплея или печатающее устройство следующие данные:

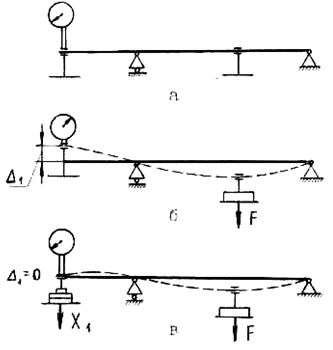
Рис. 11.2. Опытное определение лишней неизвестной

Контрольные вопросы

Определение перемещений при косом изгибе >
Другие лабораторные работы >
Примеры решения задач >