Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.
Понятие о напряжениях в точке
На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.
Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение
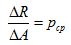
представляет собой среднее напряжение на данной площадке.
Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке
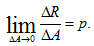
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.
Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.
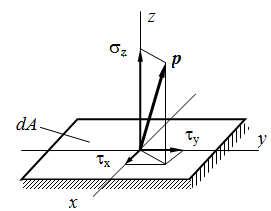
Связь между напряжениями и внутренними силами
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τx dA, τy dA.
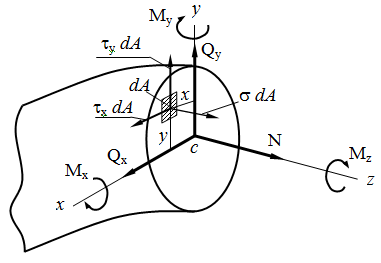
Суммируя проекции этих элементарных сил, а также их моменты относительно осей Ox, Oy, Oz, найдём;
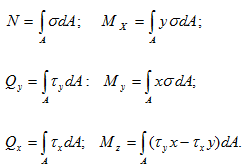
Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.
Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.
Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.
Объемное напряженное состояние
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).
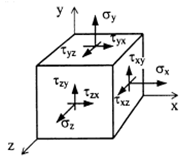
Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:
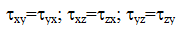
Относительные деформации и напряжения связаны обобщенным законом Гука.
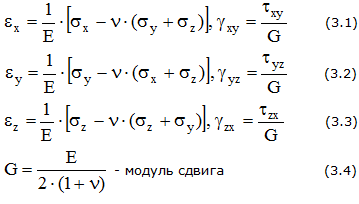
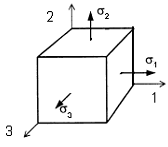
Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).
Обозначение главных напряжений:
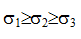
Напряженное состояние называется объемным или трехосным, если
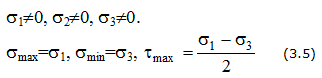
Относительное изменение объема:
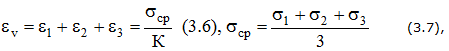
где К – модуль объемной упругости,
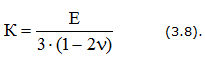
Удельная потенциальная энергия упругой деформации:
— полная
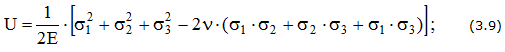
— изменение объема
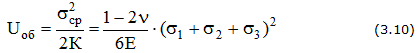
— изменение формы
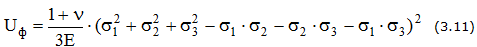
Плоское напряженное состояние
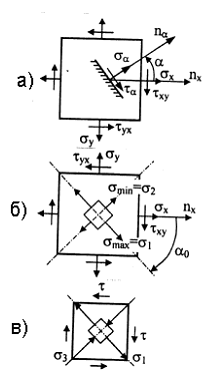
Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).
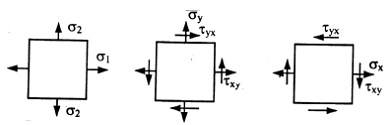
Напряжения на наклонной площадке (рис. 3.4,а)
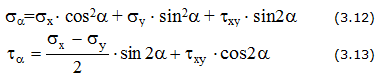
Величина и направление главных напряжений (рис. 3.4,б)
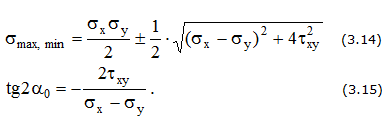
Чистый сдвиг σx = σy = 0 (рис. 3.4,в)
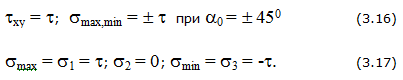
Линейное напряженное состояние
Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.
Проверка прочности при линейном напряженном состоянии проводится по условию прочности:
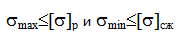
В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:
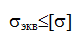
Величина σэкв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.
Гипотезы прочности
Существует 5 гипотез прочности:
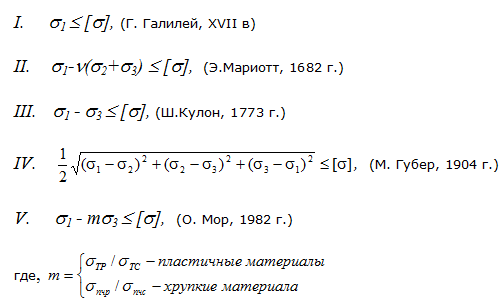
Далее: