Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.
Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.
При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.
В результате имеем следующие уравнения статики:
- Сумма проекций всех сил на вертикальную ось равна нулю
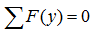
- Сумма моментов относительно любой точки системы тоже равна нулю.
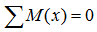
Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.
Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.
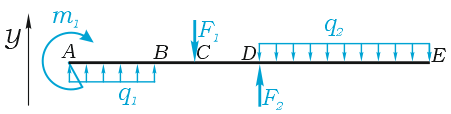
Уравнения статики
Сумма проекций всех сил на ось Y:
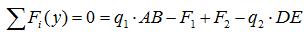
Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.
Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.
Проекции сил на ось Z в данном случае равны нулю:
Сумма моментов всех нагрузок, например, относительно точки A:
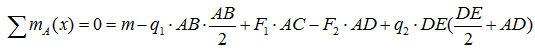
Дополнительные материалы
- Порядок определения момента от распределенной нагрузки.
- Правила знаков при составлении уравнений статики для систем находящихся в равновесии.
Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.
Уравнения равновесия >
Примеры решения задач >
Краткая теория >