Пример решения задачи по определению величины и направления полной скорости и полного ускорения при сложном движении точки колеса кривошипа.
Задача
Колесо Ⅰ с радиусом R вращается вокруг оси, проходящей через центр колеса перпендикулярно плоскости чертежа с угловой скоростью ωⅠ и угловым ускорением εⅠ.
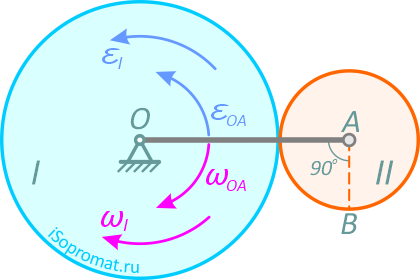
Рисунок 27
Независимо от него на той же оси вращается кривошип OA с угловой скоростью ωOA и угловым ускорением εOA. Кривошип приводит в движение колесо Ⅱ с радиусом r, которое катится по колесу Ⅰ (рисунок 27).
Найти скорость VB и ускорение aB точки B, если R = 20 см, r = 10 см, ωⅠ = 5 с−1, εⅠ = 1 с−2, ωOA = 3 с−1, εOA = 2 с−2.
Решение
Колесо Ⅰ и кривошип совершают вращательное движение, а колесо Ⅱ – плоскопараллельное движение.
Найдем скорость точки B, для этого определим положение мгновенного центра скоростей колеса Ⅱ. Чтобы найти МЦС нужно, знать направление скоростей хотя бы двух точек тела.
Найдем скорость точки A, которая принадлежит колесу Ⅱ и кривошипу OA.
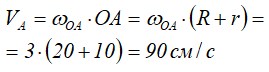
Вектор VA направлен перпендикулярно отрезку OA в сторону вращения кривошипа (рисунок 28).
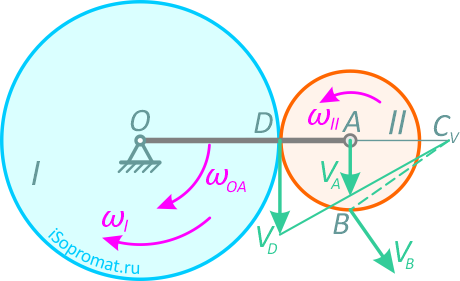
Рисунок 28
В точке соприкосновения колес скорость точки колеса Ⅱ должна равняться скорости точки колеса Ⅰ. Обозначим эту точку буквой D. Эта точка не принадлежит кривошипу OA. Так как движение колеса Ⅰ известно, можно найти скорость точки D.
![]()
Вектор скорости точки D направлен перпендикулярно радиусу OD в сторону вращения колеса Ⅰ. Таким образом, нам известны скорости двух точек колеса Ⅱ. Проведем перпендикуляр к скоростям в точках A и D и прямую, проходящую через концы векторов скоростей VD и VA.
В точке пересечения этих линий и будет МЦС для колеса Ⅱ. Обозначим его буквой CV.
Найдем расстояние ACV:
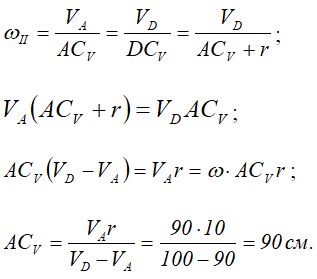
Тогда
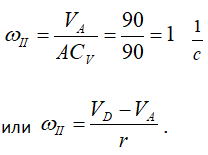
Зная угловую скорость колеса Ⅱ и его МЦС, найдем скорость точки B.
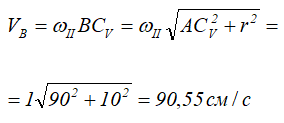
Вектор VB направлен перпендикулярно отрезку BCV в сторону вращения колеса Ⅱ.
Определим ускорение точки B.
Согласно теореме, ускорение точки B определятся по формуле
![]()
где aA — ускорение точки A, принятой за полюс;
aBA — ускорение точки B во вращательном движении, вокруг полюса A.
Точка A принадлежит кривошипу OA – движение которого известно, тогда
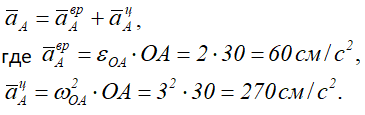
Вектор aτA — направлен перпендикулярно OA, в сторону, обратную VA, т.к. вращение кривошипа по условию задачи замедленное.
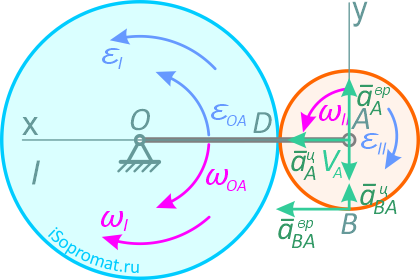
Рисунок 29
Вектор anA — направлен от A к O.
Вектор
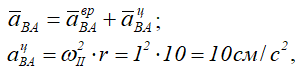
и направлен от точки B к полюсу A.
![]()
Для его вычисления найдем угловое ускорение εⅡ:
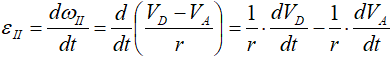
r – в задачах такого типа величина постоянная, выносится за знак производной:
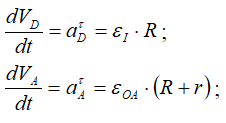
Отсюда
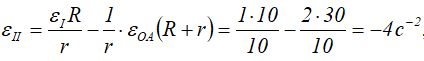
Знак «−» говорит о том, что вращение колеса Ⅱ замедляется.
Величина
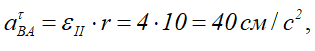
и направлена перпендикулярно anBA. Полное ускорение найдем, сложив все слагаемые:
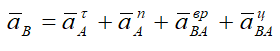
Направив ось AX вдоль AO, ось AY перпендикулярно AO, получим:
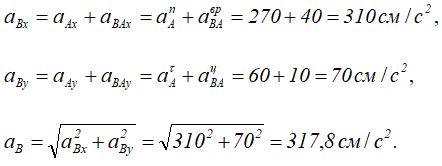
Вектор aB составляет с осью AХ угол α, косинус которого
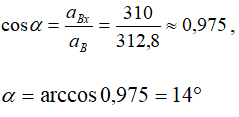
а с осью AY угол β, косинус которого:
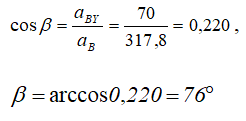
Далее: