Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, в момент времени, когда угол положения кривошипа будет равен заданному значению.

Задача

Кривошип OA, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку O, приводит в движение колесо Ⅱ, которое катится без скольжения по неподвижному колесу Ⅰ.

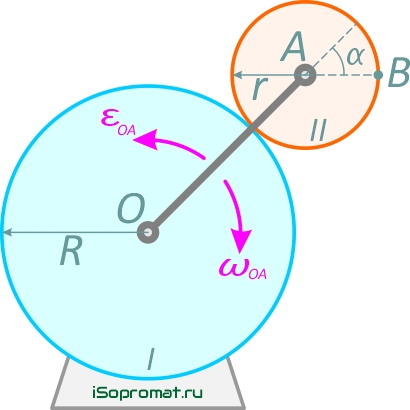
Рисунок 9

Найти скорость и ускорение точки B колеса Ⅱ, для момента времени, когда угол α = 45°, если R = 40 см, r = 20 см, ω_OA = 4 с⁻¹, ε_OA = 2 с⁻² (рисунок 9).

Теория по теме задачи

Решение

Колесо Ⅱ движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.

По условию, колесо Ⅰ неподвижно, значит, точка соприкосновения колес является МЦС для колеса Ⅱ.

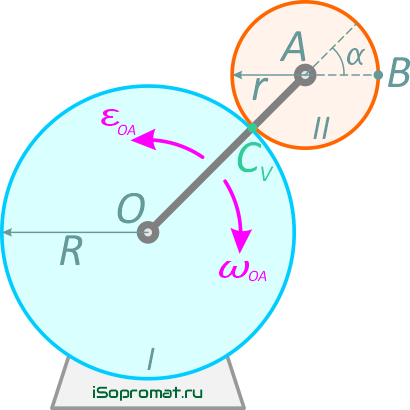
Рисунок 10

Обозначим ее как C_V (эта точка не принадлежит кривошипу OA). Скорость точки B определяется выражением

и направлена перпендикулярно отрезку BC_V, в сторону вращения колеса Ⅱ (рисунок 11)

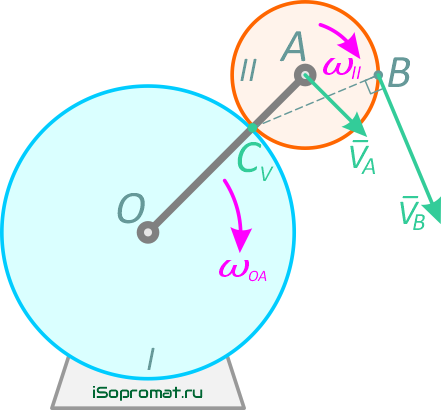
Рисунок 11

Для определения угловой скорости ω_Ⅱ запишем выражение для линейной скорости точки A.

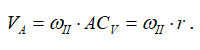
С другой стороны, точка A принадлежит кривошипу OA. Скорость точки A, принадлежащей кривошипу, определяется выражением

и направлена ⊥ OA в сторону вращения кривошипа OA. Из этих рассуждений следует:

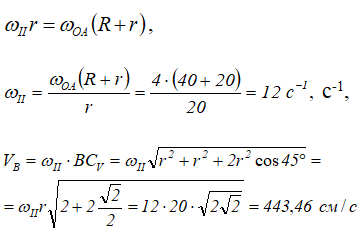
Найдем скорость точки B, используя теорему о скоростях точек плоской фигуры. Для этого примем точку A за полюс.

Тогда

Величина и направление скорости точки A определяются из условий движения кривошипа OA.

V_A = ω_OA × OA

и вектор V_A ⊥ OA и направлен в сторону вращения кривошипа (рисунок 12).

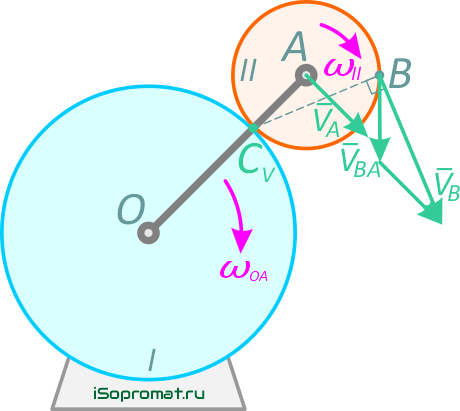
Рисунок 12

Скорость V_BA — это скорость точки B во вращательном движении вокруг полюса A.

Величина скорости

V_BA = ω_Ⅱ × r = 12 × 20 = 240 см⁄с

и этот вектор направлен перпендикулярно отрезку AB в сторону вращения колеса Ⅱ.

Чтобы сложить векторы V_A и V_BA, перенесем вектор V_A в конец вектора V_BA. Соединяя начало вектора V_BA с концом вектора V_A, получим вектор V_B. Из построения:

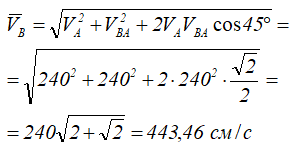
Определим ускорение точки B, совершающей сложное движение.

Согласно теореме об ускорении точки плоской фигуры, ускорение точки B можно определить из выражения

где a_A — ускорение точки A, принятой за полюс;

a_BA — ускорение точки B во вращательном движении, вокруг полюса A.

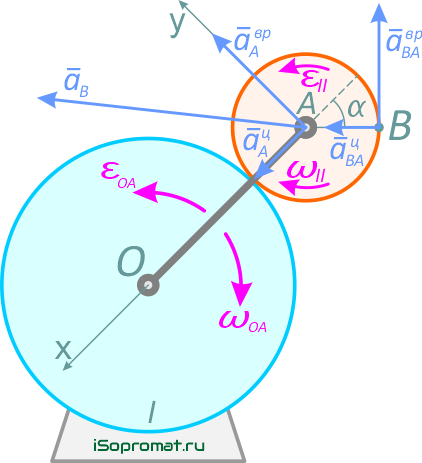
Рисунок 13

Точка A – принадлежит колесу Ⅱ и кривошипу OA, движение которого известно, тогда

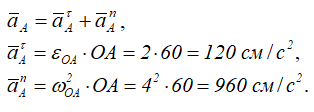
Ускорение a_BA (ускорение во вращательном движении) состоит из двух слагаемых:

где

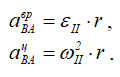
Найдем угловое ускорение второго колеса ε_Ⅱ по определению:

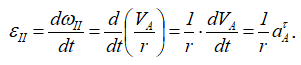
Подставляя числовые значения, получим

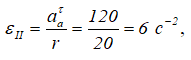
тогда

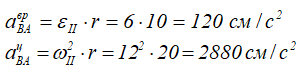
Ускорение точки B найдем, спроецировав все векторы уравнения

на выбранные оси координат OX и OY.

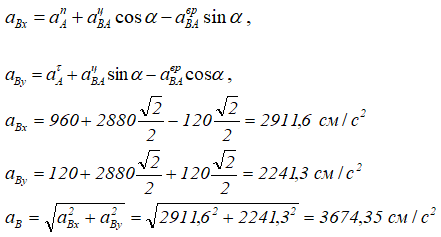
Углы, которые составляют вектор ускорения a_B с осями OX и OY, определим через направляющие косинусы.

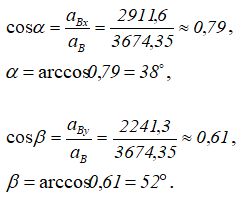
Скорость и ускорение точки B колеса Ⅱ, для момента времени, когда угол α = 45° найдены.

---

Далее: