Решение задачи (РГР) Д19 «Применение общего уравнения динамики к исследованию движения механической системы с одной степенью свободы» по теоретической механике.
Пример расчета ускорения груза и натяжения нитей для заданной механической системы, движущейся из состояния покоя, без учета моментов сопротивления в подшипниках и массы нерастяжимых нитей.
Задача
Для заданной механической системы определить ускорение груза и натяжения нитей.
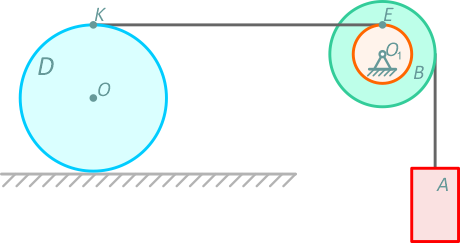
Система движется из состояния покоя, моменты сопротивления в подшипниках не учитывать, массами нитей пренебречь, нити не растяжимы (рис. 2.1).
Дано: mA, mB, RB, rB, i, mD, RD, fk;
i – радиус инерции блока B, при вращении его вокруг оси перпендикулярной плоскости чертежа;
fk – коэффициент трения качения для катка D;
каток D – сплошной однородный цилиндр.
Пример решения
Определим направление движения системы, указав направление ускорения груза A, покажем на рис. 2.2. задаваемые силы: GA, GB, GD реакции связей NB, ND (направление NB пока неизвестно). Силы инерции для тела A приводятся к главному вектору сил инерции ФА=mA∙aA, для тела B к главному моменту сил инерции MBФ=JB∙εB, для тела D, совершающего плоское движение к главному вектору сил инерции ФD=mD∙aD и к главному моменту сил инерции MDФ=JD∙εD. Коэффициент трения качения определяет наличие момента сопротивления
![]()
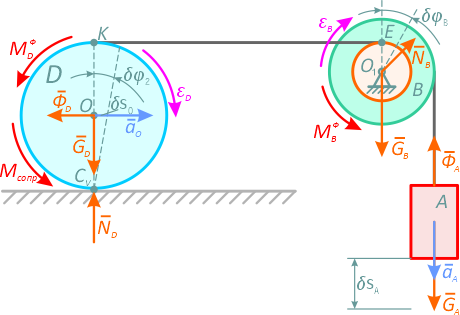
Ускорения и перемещения точек системы получаются дифференцированием и интегрированием зависимостей между линейными и угловыми скоростями точек системы.
Приняв скорость груза VA, получим соотношения
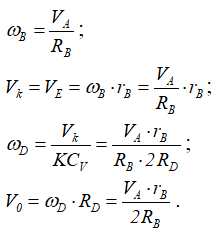
Можно продифференцировать и проинтегрировать выше приведенные формулы и получить выражения
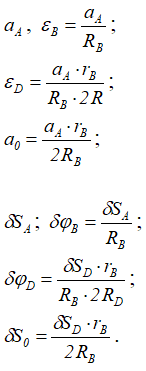
Сообщим системе возможное перемещение в направлении ее действительного движения. Силы и моменты, действующие на систему, совершат элементарную работу. Сумма всех работ должна быть равна нолю. Момент сопротивления отнесем к внешним воздействиям. Это позволит считать данную систему идеальной. Составим общее уравнение динамики (уравнение работ):
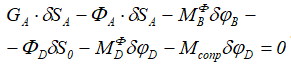
Подставим данные задачи и получим:
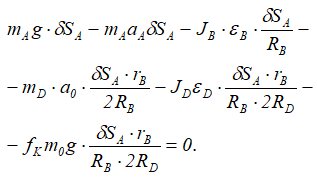
Сократив на δSA — задаваемое нами возможное перемещение груза А получим:
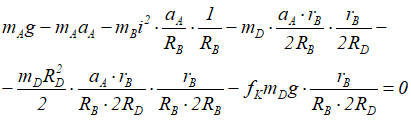
Из этого соотношения определим ускорение груза
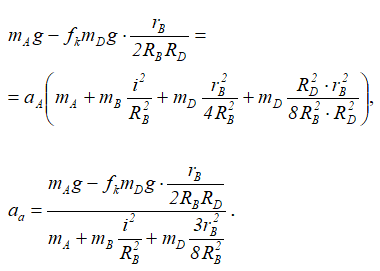
Из найденных ранее соотношений можно определить: εB, a0, εD.
При решении задачи этим методом внутренние силы в уравнения не входят. Для определения натяжения нитей нужно сделать эти силы внешними, для чего разделяем систему на части.
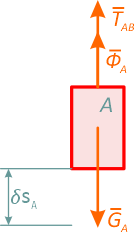
Рассмотрим отдельно груз А, на который действуют силы ФA, GA и сила TAB, ставшая внешней (рис. 2.3). Для этой системы можно написать или принцип Даламбера
![]()
или общее уравнение динамики.
![]()
Находим натяжение нити:
![]()
Для определения натяжения нити между телами B и D можно составить общее уравнение динамики (или написать принцип Даламбера) для тела B или D.
Рассмотрим тело D (рис. 2.4). Покажем действующие внешние силы и силы инерции. Натяжение нити ТBD стало внешней силой.
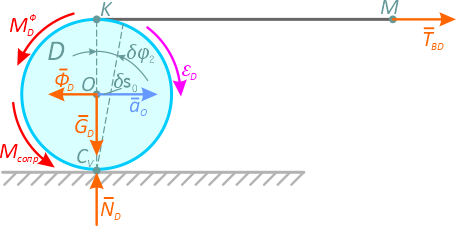
Приняв за возможное перемещение угол поворота тела D — δφD составим уравнение работ.
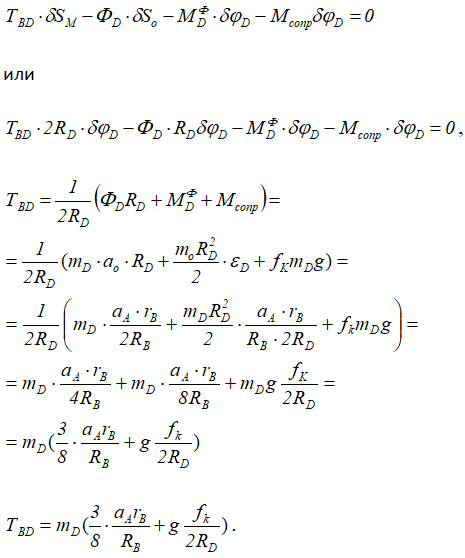
Для проверки результатов можно написать общее уравнение динамики (или принцип Даламбера) для блока B.
Далее: