Пример решения задачи по расчету положения центра тяжести сложного сечения, составленного из швеллера, уголков и пластин, симметричного относительно одной из осей.
Задача
Для симметричного составного сечения, состоящего из прокатных профилей (швеллер и равнобокие уголки) и двух прямоугольников (листовой прокат).
Другие примеры по теме >
Помощь с решением задач >
требуется:
- определить положение центра тяжести;
- вычислить значения главных центральных моментов инерции и главных радиусов инерции;
- построить эллипс инерции.
Дано:
- швеллер N16а;
- уголки равнобокие 70×70×5 (2 шт.);
- размеры листов — 160×10 мм (2 шт.).
Решение
По соответствующим сортаментам и формулам находим геометрические характеристики фигур,
- площадь сечения A;
- осевые моменты инерции Ix и Iy;
- положение z0 центра тяжести C сечений
составляющих заданное сечение:
— уголки равнобокие 70×70×5 (ГОСТ 8509-72)
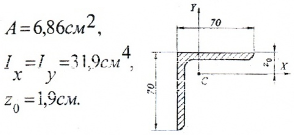
— швеллер N16а (ГОСТ 8240-72)
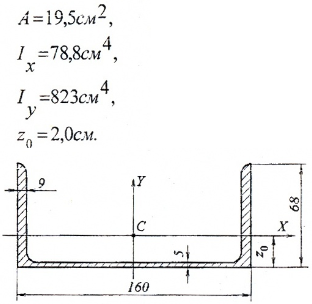
— прямоугольник 160×10 мм
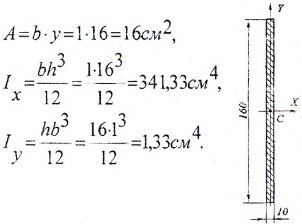
Вычерчиваем составное сечение в масштабе (например, 1:2), отмечаем центры тяжести отдельных фигур Ci и проводим их центральные оси Xi, Yi.
Положение центра тяжести и главных осей
Одной из главных центральных осей является ось симметрии YC.
Выбрав вспомогательную ось Xвсп и определив по чертежу координаты центров тяжести отдельных фигур yi относительно этой оси, находим положение главной центральной оси XC по формуле:
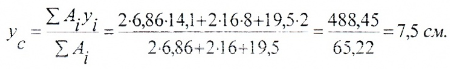
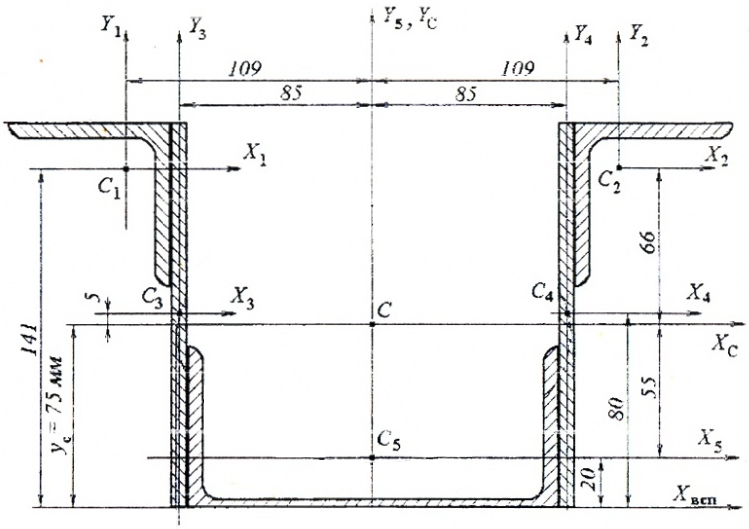
Расчет главных центральных моментов инерции
При этом пользуемся зависимостями между моментами инерции относительно параллельных осей, учитывая при этом симметричность отдельных частей сечения:
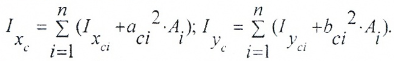
Здесь: IxCi, IyCi — моменты инерции отдельных фигур относительно собственных центральных осей;
Ai — площади самих фигур;
aCi, bCi — координаты центров тяжести фигур относительно главных центральных осей.
Учитывая вышесказанное, а также симметричность отдельных частей сечения, находим главные моменты инерции:
При большом числе элементов, составляющих сложное сечение, целесообразно для нахождения yC, IxC, IyC использовать табличную форму записи.
Расчет радиусов инерции
Главные радиусы инерции:
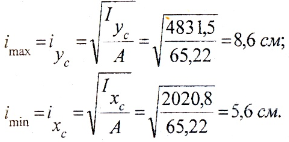
По этим данным строим эллипс инерции, накладывая его на чертеж сечения.
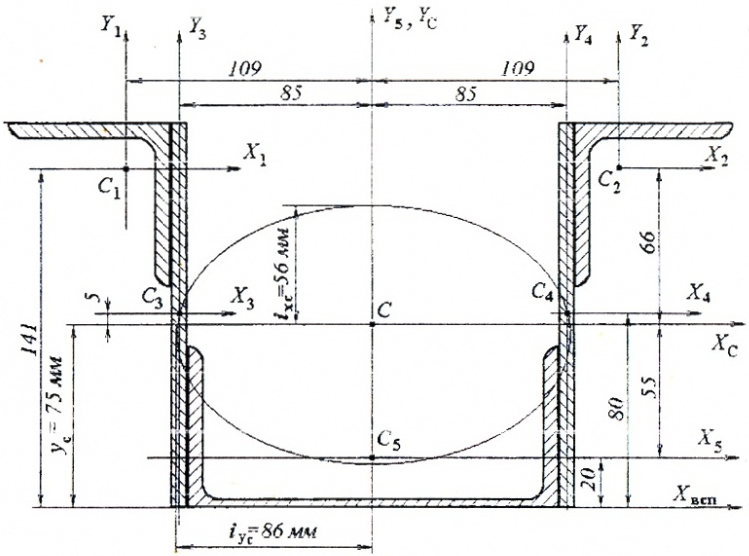
Эллипс инерции позволяет оценить правильность вычислений, его габариты обычно составляют 0,55…0,70 от габаритов сечения.
