Пример решения задачи на построение эпюры нормальных напряжений σ при изгибе стальной балки прямоугольного сечения.

Задача

Построить эпюру распределения нормальных напряжений для подобранного ранее прямоугольного сечения двухопорной балки с размерами h=155мм и b=80мм.

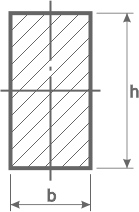
Изгибающий момент в опасном сечении балки M_{x max}=47,6кНм.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущие пункты решения задачи:

1. Определение опорных реакций,
2. Построение эпюр поперечных сил и изгибающих моментов,
3. Подбор размеров прямоугольного сечения балки.

Рассмотрим пример построения эпюры распределения нормальных напряжений в опасном сечении балки.

Прямоугольное сечение имеет три характерных точки:

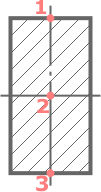
1 – верхняя,

Для построения эпюры достаточно найти значения в любых двух точках, потому что при изгибе нормальная составляющая полных напряжений по высоте сечения меняется линейно.

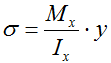
где I_x – осевой момент инерции сечения,
y – расстояние от оси х проходящей через центр тяжести сечения до точки в которой рассчитывается напряжение.

Очевидно, что на самой оси x (точка №2) где координата y=0 напряжения отсутствуют.

Наибольшие значения нормальных напряжений будут на максимальном удалении от оси x, то есть при y_max=h/2 (в точках 1 и 3).

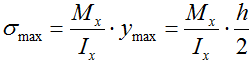
Рассчитаем момент инерции прямоугольного сечения

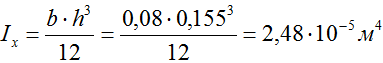
Тогда максимальные напряжения

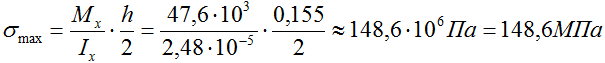
При изгибе верхний и нижний слой балки испытывают продольную деформацию разных знаков.

Знаки напряжений в точках 1 и 3 определяются по построенной ранее эпюре изгибающих моментов M_x.

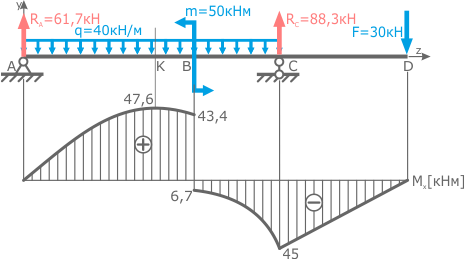
В данном случае по ней видно, что в опасном сечении балки эпюра моментов имеет положительное значение (+47,6 кНм), что согласно правила знаков при изгибе говорит о том, что в рассматриваемом месте балки сжимаются верхние слои (нижние соответственно растягиваются).

Другие видео

Поэтому в соответствии с правилом знаков для напряжений, нормальные напряжения в верхней точке 1 будут отрицательны (потому что сжатие), а в точке 3 – положительны (растяжение) или σ_т1=-148,6МПа, σ_т3=148,6МПа.

По полученным данным строим эпюру

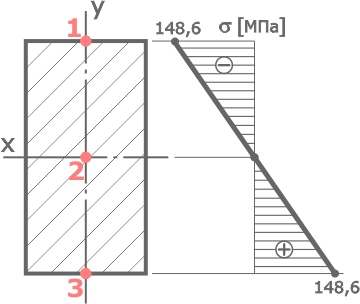
Как видно по построенной эпюре, нормальные напряжения не превышают заданных допустимых значений, что говорит о том, что размеры прямоугольного сечения были подобраны верно, и прочность балки обеспечена.

Другие примеры решения задач >