Пример решения задачи на построение эпюры нормальных напряжений σ при растяжении и сжатии стального стержня квадратного сечения.
Задача
Построить эпюру нормальных напряжений для стержня постоянного сечения, нагруженного продольными силами.
Поперечное сечение стержня — квадрат со сторонами a=22мм. Допустимые напряжения [σ]=160МПа
Другие примеры решений >
Помощь с решением задач >
Решение
Предыдущие пункты решения задачи:
- Определение опорной реакции в заделке стержня,
- Построение эпюры внутренних продольных сил,
- Подбор размеров сечения стержня по условию прочности.
Расчет нормальных напряжений при растяжении-сжатии производится по формуле:
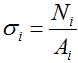
т.е. напряжения в рассматриваемом сечении определяются отношением соответствующей величины внутренней силы к площади поперечного сечения стержня.
Площадь поперечного сечения стержня постоянна по всей его длине, и составляет
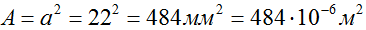
Очевидно, что в пределах участка стержня, на котором внутренняя сила и площадь постоянны, напряжения так же будут иметь одинаковую величину.
Здесь, при одинаковой площади, внутренние силы различаются на трех силовых участках. Соответственно на этих участках нормальные напряжения тоже будут отличаться.
Знак напряжений зависит от знака соответствующей внутренней продольной силы.
Значения внутренних сил принимаются с построенной ранее эпюры N.
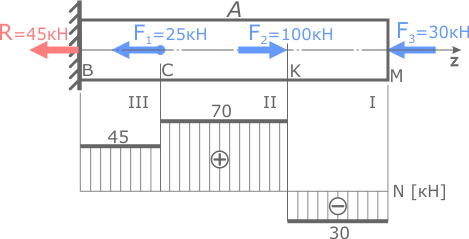
Расчет напряжений
Нормальные напряжения на I силовом участке (KM)
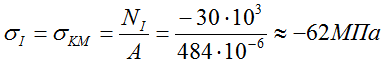
На II участке (CK)
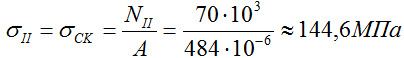
На III участке (BC)
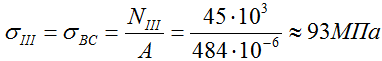
По этим данным строим эпюру нормальных напряжений.
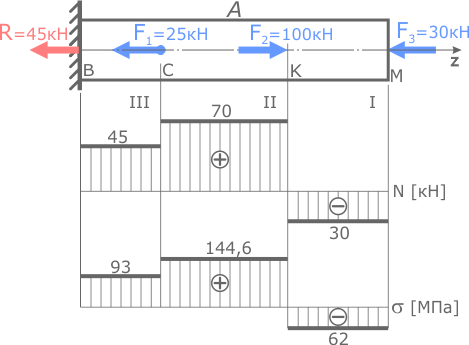
По построенной эпюре видно, что напряжения не превышают заданных допустимых значений, следовательно, рассчитанные размеры стержня обеспечивают его прочность.
