Пример решения задачи на расчет и построение эпюры перемещений сечений стержня при растяжении и сжатии.
Задача
Рассчитать перемещения характерных сечений стержня постоянного сечения и построить их эпюру.
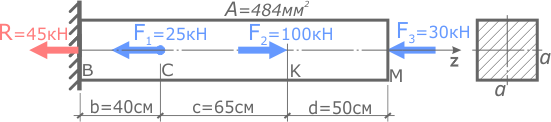
Пример решения
Предыдущие пункты решения задачи:
- Расчет опорной реакции стержня,
- Расчет внутренних сил с построением эпюры,
- Подбор размеров поперечного сечения,
- Построение эпюры напряжений,
- Расчет деформаций участков стержня.
Под действием внешних сил стержень деформируется, вследствие чего его поперечные сечения перемещаются (в данном случае влево либо вправо).
Для расчета величины и направления перемещений воспользуемся соответствующей формулой:
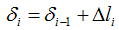
где δi – перемещение рассматриваемого сечения,
δi-1 – перемещение предыдущего сечения,
Δli – деформация участка расположенного между указанными сечениями (рассчитаны ранее).
По расчетной схеме видно, что сечение, расположенное в заделке (сечение B) перемещаться не может, следовательно, его перемещение равно нулю, т.е.
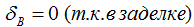
Перемещение остальных сечений рассчитывается последовательно от него.
Следующим рассматриваем сечение C.
Его перемещение δC будет складываться из двух составляющих:
- изменения дины участка BC,
- перемещения предыдущего сечения B с которым связан их общий участок.
Так как сечение В неподвижно, сечение C переместится ровно на ту величину, на которую растянется III участок BC.
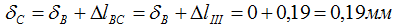
Перемещения остальных сечений рассчитываются аналогично:
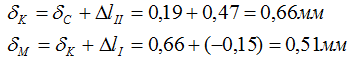
По этим данным строится эпюра перемещений δ. Для этого рассчитанные значения в выбранном масштабе откладываются от базовой линии под соответствующим сечением стержня.
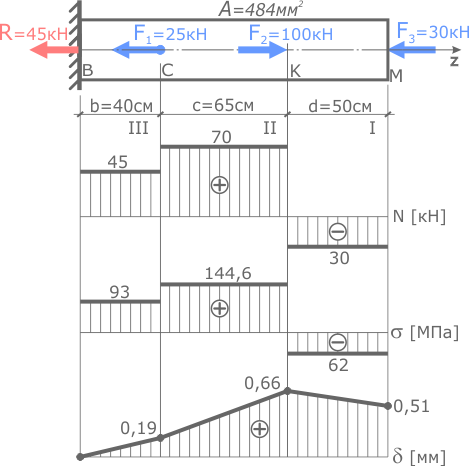
Эпюра наглядно показывает, что в результате деформации стержня наибольшее перемещение получило сечение K, которое переместилось вправо на 0,66 мм, а общая длина всего стержня увеличилась на 0,51 мм.
На участках, где нормальные напряжения положительны линия эпюры перемещений идет на возрастание (при условии, что заделка слева) и, наоборот. При этом, чем больше величина напряжений, тем больше угол наклона линии эпюры δ к базовой линии.
Далее: