Выполним проверку построенных эпюр внутренних силовых факторов для рамы с помощью дифференциальных зависимостей и условий равновесия вырезанных узлов рамы (узловая проверка).
Геометрическая проверка
Начнем с геометрической проверки по дифференциальным зависимостям.
Проверка эпюры N
Проверка эпюры продольных сил N:
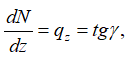
где γ – угол наклона касательной к эпюре N относительно оси абсцисс силового участка;
qz — продольная распределенная нагрузка.
В рассматриваемом примере на всех участках qz=0 и, следовательно,
tg γ=0=const,
т.е. эпюра N ограничена прямыми линиями, параллельными базовым линиям.
Проверка эпюры Q
Проверка эпюры поперечных сил Q:
На стойках AC и BD эпюра поперечных сил Q ограничена прямыми линиями, параллельными базовым линиям, т.к. нет распределенных нагрузок и tgα=0=const.
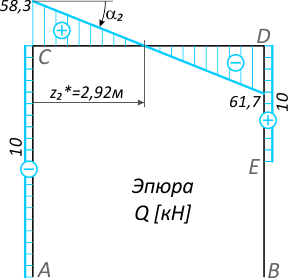
На ригеле CD
tg α2 = -(58,3+61,7)/6=-20кН/м=-q=const
— прямая с отрицательным углом наклона к оси абсцисс участка.
Проверка эпюры M
Проверка эпюры изгибающих моментов M:
На стойке AC
tg β1 = -60/6= -10кН=const
— прямая с отрицательным углом наклона к оси абсцисс.
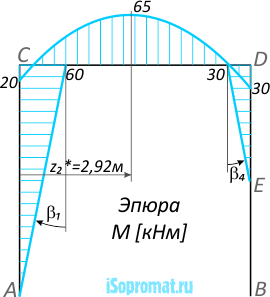
На ригеле CD эпюра изгибающих моментов M – кривая (парабола) в сечении C при ординате MC=M0=20кНм (сжаты нижние слои ригеля), угол наклона касательной к оси абсцисс положителен (против часовой стрелки) и равен
tg βC=(58,3),
что соответствует ординате QC=58,3кН.
С изменением координаты x ордината Q уменьшается до нуля, а следовательно и угол β стремится к нулю в сечении экстремума при ординате M(2,92м)=65кНм.
После экстремума угол наклона касательной становится отрицательным и в сечении D равен:
βD=arctg(-61,7),
при ординате z=6м:
MD=M(6м)=30кНм (сжатие нижних слоев).
Кривая получается выпуклостью вверх, т.е. навстречу действию распределенной нагрузки на ригеле CD.
На участке ED стойки BD:
tg β4=30/3=10кН,
β4=arctg(10)=const
— прямая с положительным углом наклона к оси абсцисс с началом при ординате ME=0 и концом при MD=30кНм (сжатые слои с внутренней стороны рамы).
Проверка равновесия узлов рамы
Рассмотрим равновесие узлов рамы.
Мысленно вырежем из заданной рамы узел C с приложенным к нему внешним моментом m=40кНм.
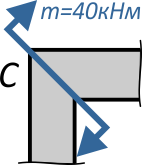
В сечениях по стойке AC и ригелю CD прикладываем к узлу векторы внутренних усилий N и Q с учетом знаков и величины.
Действие внутренних изгибающих моментов M направляем в сторону сжатых слоев в окрестности узла C:
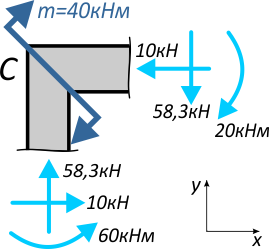
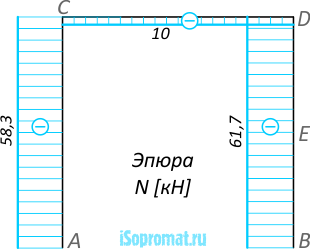
На эпюре N (рис. 1) видно, что в точке C на вертикальную часть AC действует сжимающая сила 58,3кН, на горизонтальную часть – сжимающая сила величиной 10кН.
На узле C эти силы показаны продольными и сжимающими для фрагментов соответствующих стержней.
С эпюры Q (рис. 2) принимаем значения поперечных сил в точке C:
— на вертикальной части – отрицательная сила величиной 10кН, следовательно, по правилу знаков стремится повернуть узел против хода часовой стрелки;
— на горизонтальный фрагмент узла действует положительная поперечная сила 58,3кН, следовательно, направляем ее «вниз», т.к. она стремится повернуть узел по ходу ЧС.
Эпюра M (рис. 3) была построена на сжатых слоях рамы. По ней видно, что внутренние изгибающие моменты (60кНм и 20кНм) в окрестности точки C стремятся сжать внутренние слои рамы, поэтому направляем так, как показано на рисунке (рис. 5).
Запишем уравнения равновесия:
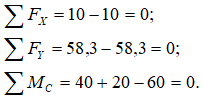
Во всех трех направлениях, усилия, приложенные к узлу C, уравновешены.
Проверим равновесие узла D.
Внешних сосредоточенных сил и момента в точке D нет, поэтому прикладываем к центрам тяжести сечений рамы только векторы внутренних усилий N и Q и показываем действие внутренних изгибающих моментов M.
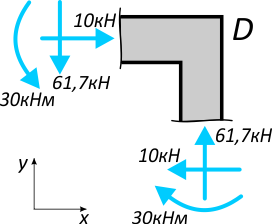
Записываем и проверяем условия равновесия:
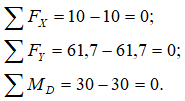
Проверки показали, что эпюры в раме построены правильно.
Далее: