В основу силового расчета механизмов по методу Н.Г. Бруевича положен принцип кинетостатики: если ко всем внешним действующим на звенья механизма силам добавить силы инерции и моменты сил инерции, то механизм будет находиться в состоянии статического равновесия.
Силовой расчет проводится по группам Ассура, начиная с наиболее удаленной от начального механизма. Заканчивается рассмотрением кривошипа, входящего в начальный механизм, для которого определяют уравновешивающую силу или уравновешивающий момент.
Для различных структурных групп Ассура разработаны специальные методы их силового исследования. В таблица 3 приведены рекомендации по анализу структурных групп II класса 1, 2, 3, 4, 5 видов.
Таблица 3 – Силовой анализ групп Ассура II класса
| Вид группы |
Заменить реакцию R12 составляющими n и τ
Заменить реакцию R43 составляющими n и τ
|
Составить | Определить |
| группа 1 вида |
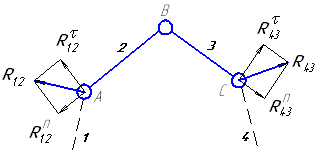 |
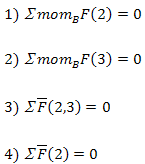 |
 |
| Заменить реакцию R12 составляющими | Составить | Определить | |
| группа 2 вида |
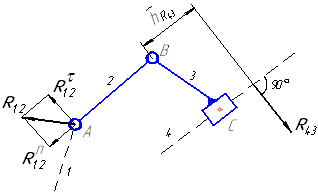 |
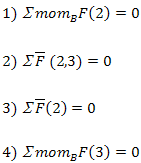 |
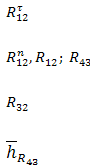 |
| Заменить реакцию R12 составляющими | Составить | Определить | |
| группа 3 вида |
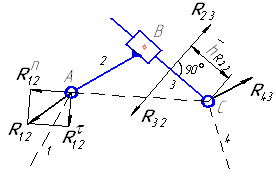 |
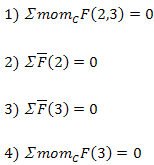 |
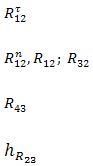 |
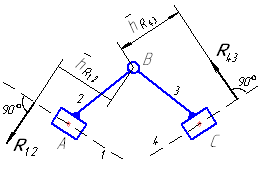
| группа 4 вида |
 |
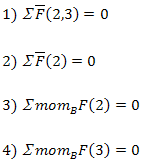 |
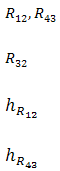 |
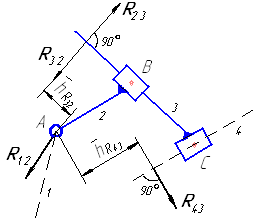
| группа 5 вида |
 |
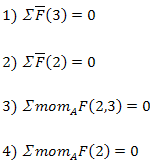 |
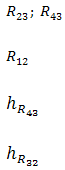 |
Рассмотрим последовательность силового расчета для заданного примера (рисунок 1). Все группы Ассура и кривошип начального механизма вычерчиваем отдельно (в масштабе) в том положении, которое они занимают на механизме в рассматриваемый момент времени.
Прикладываем к ним все силовые факторы, включая реакции в кинематических парах. Реакции во вращательных парах (шарнирах) неизвестны по величине и направлению, поэтому первоначально направляем их произвольно. Реакция в поступательной паре (ползуне) направлена перпендикулярно направляющей (т.к. вначале расчет ведется без учета сил трения), но неизвестны величина и точка приложения этой реакции.
Сила полезного сопротивления Fп.с. всегда направляется против скорости точки приложения этой силы, а момент сил полезного сопротивления Мп.с. – против угловой скорости звена приложения этого момента.
Группа (4,5) второго класса третьего вида
На звено 5 действует момент полезного сопротивления Мп.с., который направляется противоположно ω5 в данном положении механизма (если звено 5 движется поступательно, то действует сила полезного сопротивления Fп.с., которая направлена против скорости этого звена).
Одну из крайних реакций (в данном примере R65 в шарнире Е) раскладываем на две составляющие:
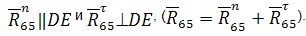
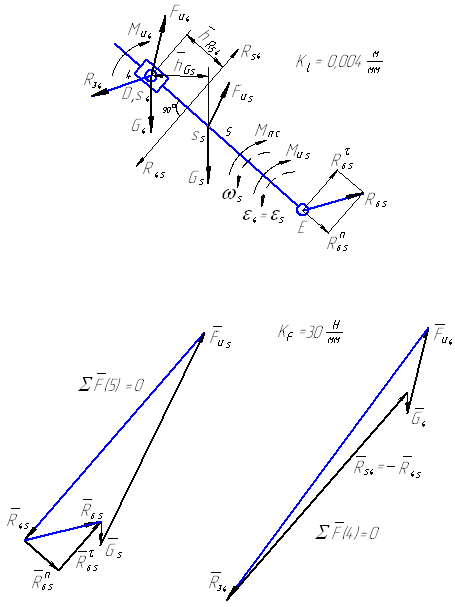
Рисунок 8 – К силовому расчету по методу Н.Г. Бруевича группы Ассура II класса 3 вида
Составляем четыре уравнения равновесия:
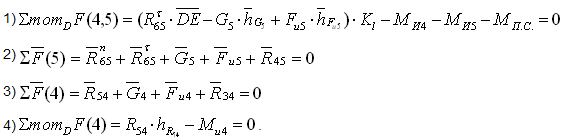
Решая первое уравнение, определяем Rτ65. Если реакция Rτ65 получится отрицательной, значит ее фактическое направление противоположно предварительно принятому. Второе и третье уравнения решаются графически построением планов сил в выбранном масштабе Kl (рисунок 8).
При этом во втором уравнении неизвестными являются величины реакций Rn65 и R45 при известном их направлении (Rn65||DE, R45⊥DE). Пересечением этих векторов при построении плана получаем их величины. В третьем уравнении R54=-R45, а вектор R34 неизвестен ни по величине, ни по направлению и при построении плана сил определяется как замыкающий вектор.
Решая четвертое уравнение, определяем точку приложения реакции R54 (истинное значение плеча hR54 в метрах).
Группа (2,3) второго класса первого вида
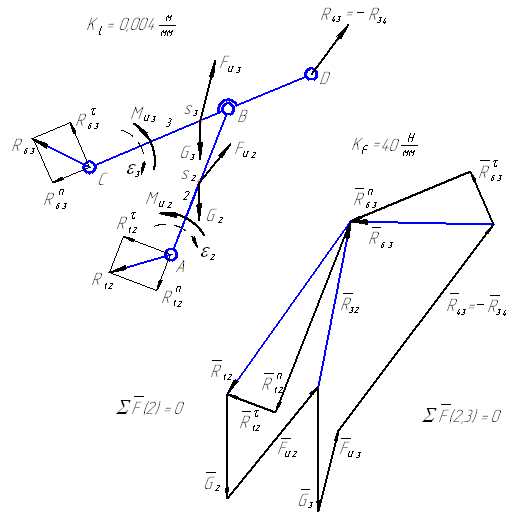
Рисунок 9 – Кинетостатика группы Ассура II класса 1 вида (звенья 2 и 3)
При решении этой группы (рисунок 9) также составляем четыре уравнения равновесия, из которых определяем реакции в кинематических парах (шарнирах) А, В и С. Реакция в шарнире D является теперь известной внешней силой (R43=-R34). Графическая часть решения приводится на рисунке 9.
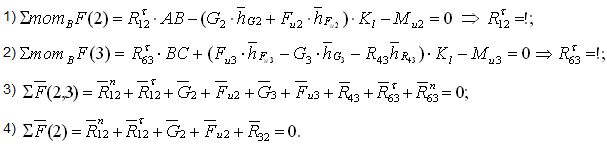
Примечание: в данном примере план сил, действующих на звено 2, для определения реакции R32 представлен как часть общего плана для группы 2,3 (левая часть общего плана).
Завершаем силовой расчет по методу Н.Г. Бруевича рассмотрением равновесия кривошипа 1 (начальное звено анализируем последним). Для определения реакции R61 строим план сил по уравнению
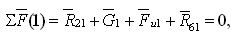
где R21=-R12.
Из уравнения
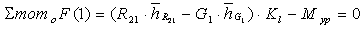
определяем уравновешивающий момент Мур (в данном случае движущий момент, необходимый для преодоления всех сил, включая МП.С., и обеспечивающий при этом заданный закон движения на входе ω1 = const).
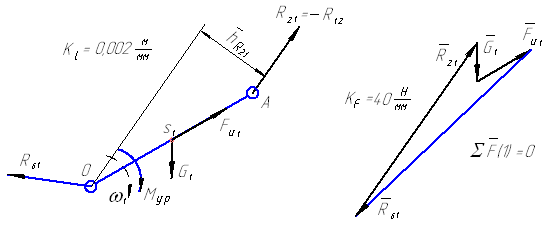
Рисунок 10 – К кинетостатике кривошипа 1
Далее: