Опорными называют реакции связей, возникающие в опорах под действием внешних нагрузок и удерживающие рассматриваемый элемент или конструкцию в статическом равновесии.
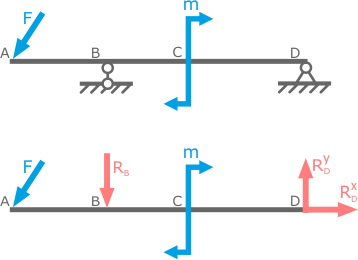
При расчете элементов конструкций реакции опор также выступают в качестве внешних усилий приложенных к рассматриваемому телу.
Подрообнее о реакциях в различных типах опор смотрите в нашем видео:
Вопрос определения опорных реакций подробно рассматривается в курсе теоретической механики, но на практике часто применяется и при решении задач сопротивления материалов.
При этом некоторые задачи в сопромате можно решить без их определения. Это возможно в случаях, когда за расчетную схему принимается брус, закрепленный в жесткой опоре (заделке) без дополнительных опор, например, статически определимые консольные балки, стержни либо стержневые системы.
Реакции в шарнирных опорах
Реакции в шарнирных опорах могут возникать только по тем направлениям, в которых перемещение исключено:
нормально к опорной поверности и вдоль неё.
Моменты в шарнирных опорах не возникают.
Подробные примеры расчета реакций в опорах
Реакции в шарнирно-неподвижных опорах
В плоской шарнирно-неподвижной опоре исключены линейные перемещения во всех направлениях и возможен только поворот относительно шарнира.
Поэтому в таких опорах могут иметь место реакции, направленные нормально к поверхности и вдоль нее:
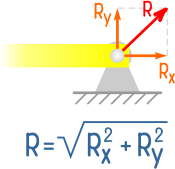
Они являются проекциями полной реакции R на вертикальную и горизонтальную оси.
Реакции в шарнирно-подвижных опорах
В шарнирно-подвижной опоре возможно поступательное перемещение вдоль одной из осей, следовательно в данном направлении реакции быть не может.
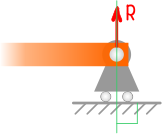
В данном случае, оставшаяся реакция по величине и направлению, будет равна полной.
Реакции в шарнире
В трехмерном шаровом шарнире аналогично, осевые проекции полной реакции R направляются вдоль всех трех осей:
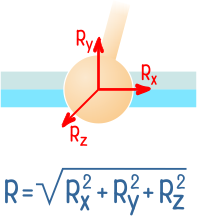
При этом, в зависимости от схемы нагружения, некоторые из проекций могут быть равны нулю.
Расчет реакций в опорах
Количество и направление реакций зависит как от вида опор, так и от способа нагружения бруса и для статически определимых систем определяются из уравнений равновесия конструкции или ее элементов.
Примеры расчета реакций опор >
Для общего случая нагружения (пространственных систем), при котором может возникать до 6 реакций опор, требуется соответствующее количество уравнений.
Например, из условия, что заданная система относительно опор не перемещается в пространстве (вправо-влево, вверх-вниз, и вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.
∑F(y)=0;
∑F(z)=0.
Из условия, что система не вращается, приравниваем к нулю суммы моментов всех нагрузок относительно соответствующих осей.
∑m(y)=0;
∑m(z)=0.
Совместное решение системы полученных уравнений позволяет определить величину и направление реакций в опорах.
Для плоской системы нагружения можно составить максимум три уравнения равновесия для определения до трех искомых усилий в опорах.
Линейно нагруженные элементы позволяют записать лишь одно уравнение равновесия.
Для расчета реакций опор статически неопределимых систем помимо уравнений статики требуются дополнительные зависимости, связывающие усилия с соответствующими им деформациями.
В некоторых случаях опорные реакции могут быть равны нулю. Это говорит лишь о том, что внешние нагрузки и остальные реакции взаимно уравновешены таким образом, что система может оставаться статичной и без соответствующего усилия в данной точке.
Далее: