Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
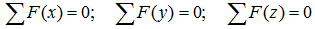
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
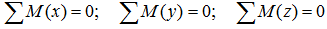
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
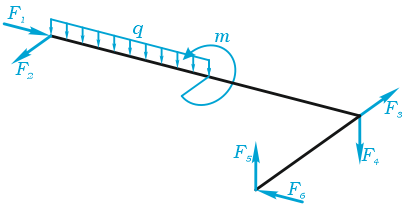
Пример составления уравнений равновесия
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
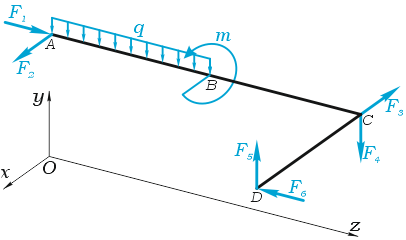
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
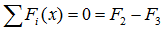
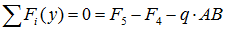
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
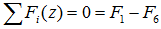
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
- в плоскости xOy:
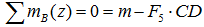
- в плоскости xOz:
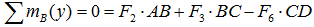
- в плоскости yOz:
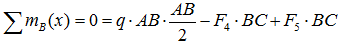
Определение момента от распределенной нагрузки рассмотрено здесь.
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
- Примеры решения задач на равновесие
- Составление уравнений равновесия
Далее: