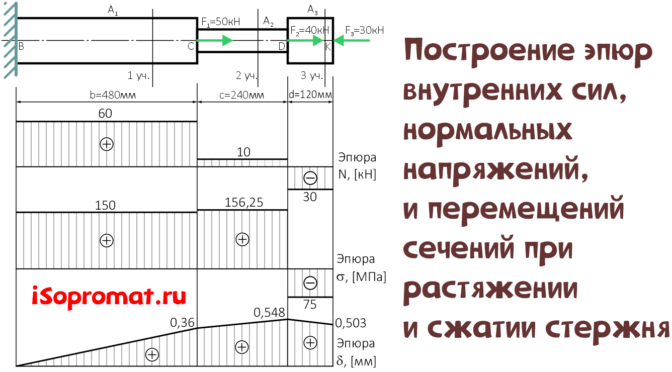
Рассмотрим примеры решения задач по построению эпюр внутренних продольных сил N, нормальных напряжений σ и линейных перемещений сечений δ [Δ] при растяжении и сжатии стержней для различных способов нагружения:
- При действии только сосредоточенных сил (2 варианта);
- С продольно распределенной нагрузкой;
- С учетом собственного веса бруса
с пояснениями выполняемых расчетов и графическими построениями.
Построение эпюр продольных сил, нормальных напряжений и перемещений сечений стержня
Задание
Для прямого ступенчатого стального стержня, испытывающего деформации растяжения-сжатия, изображенного на расчетной схеме при заданных осевых нагрузках F1, F2 и F3, площадях поперечного сечения A1, A2 и A3 и продольных размерах b, c и d, требуется:
- Определить внутренние продольные силы N по участкам и построить их эпюру,
- Вычислить величину нормальных напряжений на каждом участке, построить их эпюру по длине стержня,
- Определить продольную деформацию отдельных участков и всего стержня в целом и построить эпюру продольных перемещений.
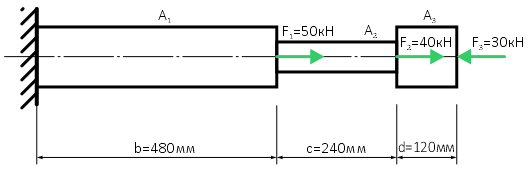
Дано: продольные осевые силы: F1=50кН, F2=40кН и F3=30кН;
Площади поперечного сечения участков стержня: A1=400мм2, A2=64мм2 и A3=400мм2;
Длина участков: b=480мм, c=240мм и d=120мм.
Принять: модуль продольной упругости материала стержня E=2∙105МПа
Решение
Вычерчиваем заданную расчетную схему растяжения-сжатия в масштабе, указываем числовые значения приложенных нагрузок и продольных размеров.
Обозначаем:
- силовые участки стержня;
- площади поперечного сечения буквой A с соответствующим индексом;
- характерные сечения стержня, начиная от его заделки (буквами B, C, D и K).
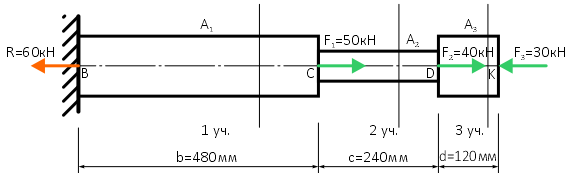
Определим опорную реакцию стержня в заделке, направив её произвольно, например, влево.
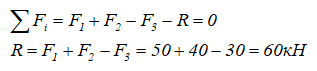
Положительное значение реакции означает, что выбранное направление оказалось верным.
Построение эпюры продольных сил N
Стержень имеет 3 силовых участка.
Рассчитаем величину внутренних продольных сил N по каждому участку стержня методом сечений, рассматривая его правую отсеченную часть.
По правилу знаков при растяжении и сжатии, продольные силы и нагрузки, которые стремятся растянуть рассматриваемую часть стержня, записываются положительными, а сжимающие силы со знаком «минус».
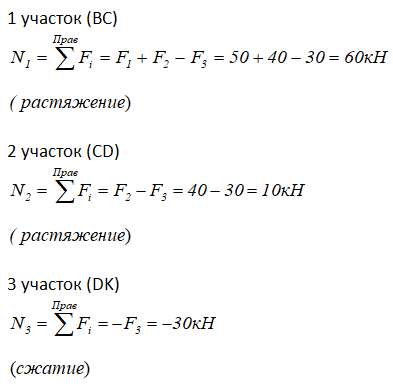
Ровно такие же значения и знаки внутренних продольных сил N можно получить, рассматривая левые от проведенного сечения части стержня
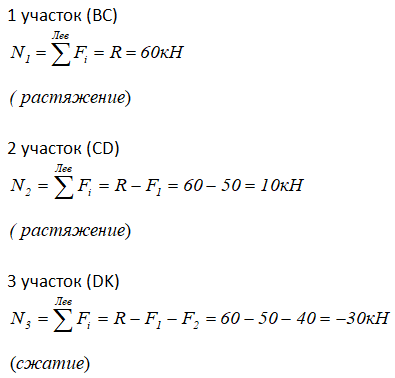
Поэтому при расчете величины внутренних силовых фактором для каждого участка можно выбирать для рассмотрения ту часть стержня, к которой приложено меньше нагрузок (при условии, что ранее была определена реакция опоры R).
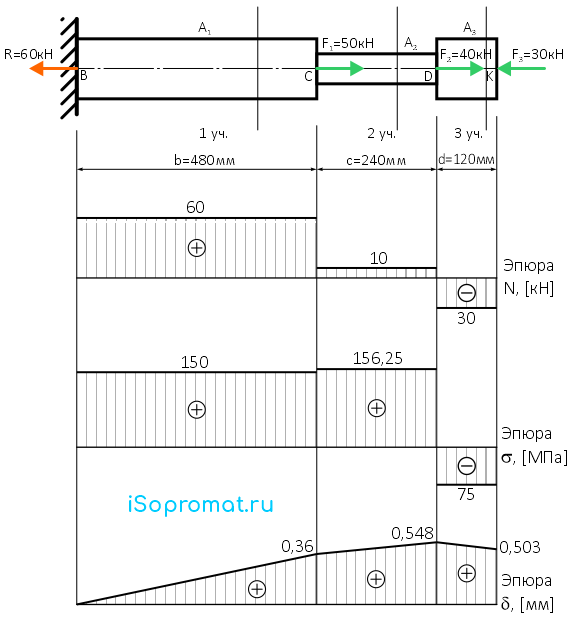
По полученным данным строим эпюру внутренних продольных сил N
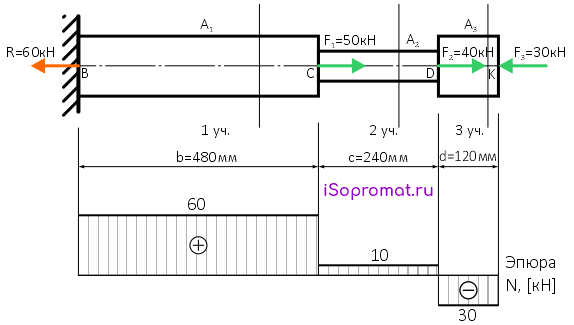
По построенной эпюре видно, что участки стержня 1 и 2 растягиваются (т.к. внутренние силы N положительны), а участок 3 сжимается (продольные силы отрицательны).
Так же на эпюре видны скачки значений внутренней продольной силы в сечениях стержня, где приложены внешние силы, включая реакцию в опоре.
Эти скачки равны величине соответствующих сил.
Значит реакция в опоре и внутренние продольные силы определены верно, а эпюра построена правильно.
Построение эпюры нормальных напряжений
Расчет величины нормальных напряжений по участкам стержня выполняется по формуле
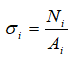
Знак нормальных напряжений зависит от знака внутренних сил N.
Рассчитаем их значения
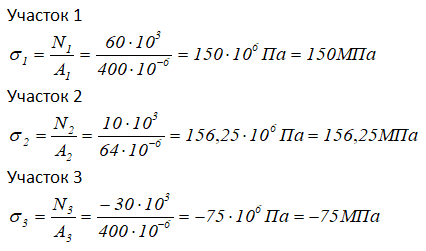
По полученным данным строим эпюру нормальных напряжений σ
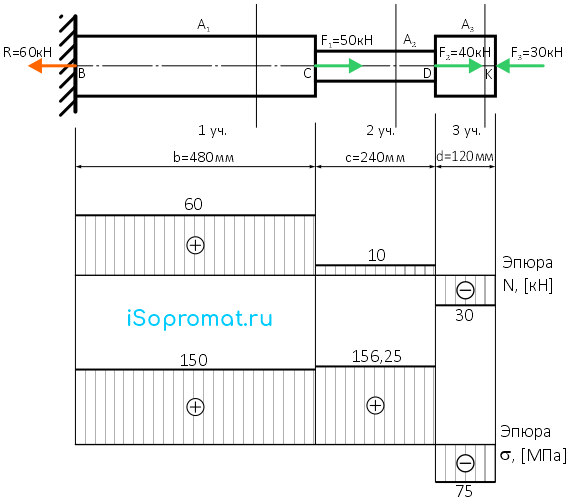
По эпюре можно проверить прочность заданного стержня, для этого все напряжения σ по модулю не должны превышать допустимых значений [σ].
Построение эпюры продольных перемещений поперечных сечений
Расчет продольных деформаций Δl участков стержня выполняется по формулам
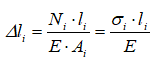
где:
l – длина рассматриваемого участка;
E – модуль продольной упругости материала, из которого выполнен стержень.
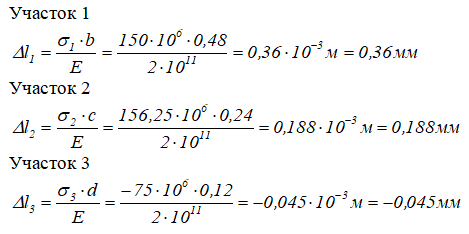
Расчет перемещений δ характерных сечений стержня проводится согласно выражения
![]()
где
δi — перемещение рассматриваемого сечения;
δi-1 — перемещение предыдущего сечения;
Δli — изменение длины участка, расположенного между этими сечениями.
В данной задаче сечение B является неподвижным, так как находится в заделке, т.е. его перемещение равно нулю
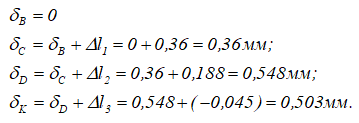
По этим данным строим эпюру продольных перемещений δ сечений стержня.
Полное изменение длины стержня можно определить, сложив с учётом знаков, деформации всех участков стержня.
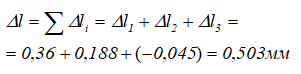
Это значение должно совпадать с перемещением крайнего правого сечения стержня.
Построение эпюр внутренних сил, напряжений и линейных перемещений бруса
Рассмотрим пример, в котором на одном из участков продольные силы и напряжения будут равны нулю, и, следовательно, соответствующие эпюры для этих частей бруса будут нулевыми.
Задача
Для расположенного горизонтально ступенчатого бруса, нагруженного силами F1 и F2, приложенными к середине участков длиной b и c, требуется построить эпюры продольной силы, напряжений и линейных перемещений точек поперечных сечений.
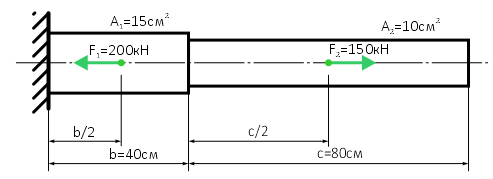
Исходные данные для решения задачи:
Нагрузки F1=200кН; F2=150кН;
Размеры сечения A1=15см2; A2=10см2;
Длина участков b=40см; c=80см;
Модуль Юнга: E=200ГПа;
Пример решения
При заданных нагрузках в опорном сечении бруса возникает только осевая составляющая реакции – R.
Из уравнения равновесия:
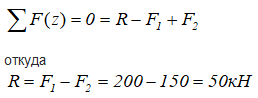
Вообще говоря, для решения поставленной задачи величину реакции R можно не определять, так как продольную силу в любом сечении можно вычислить, рассматривая только правую отсеченную часть бруса.
Расчет эпюры внутренних сил
Рассматриваемый брус имеет три силовых участка – BC, CK и KM.
Для определения величины N по участкам воспользуемся методом сечений.
Вычисляем значения продольной силы на участках:
1 участок BC
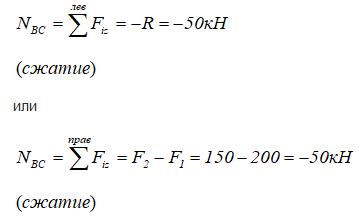
2 участок CK
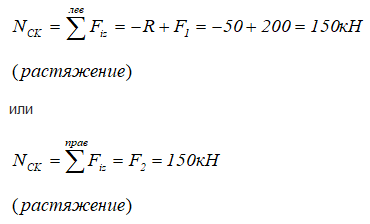
3 участок KM
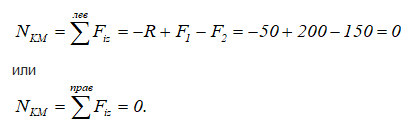
По полученным данным строим эпюру N бруса при его растяжении и сжатии
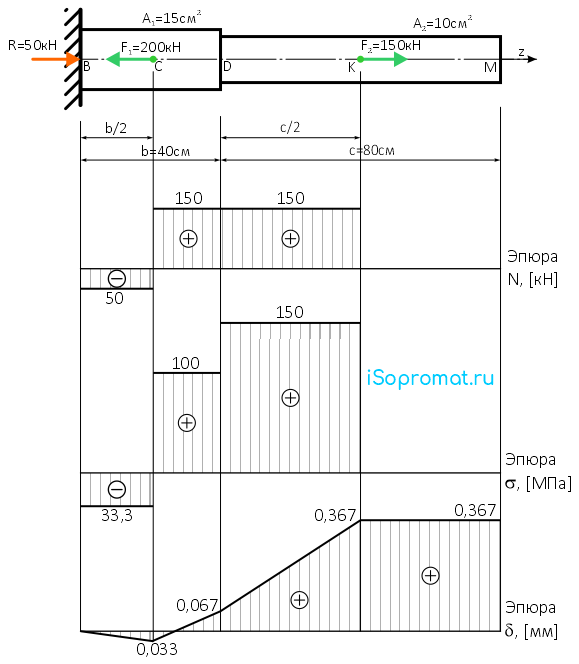
Штриховка эпюр обычно производится перпендикулярно к базовой линии, ордината эпюры указывает значение продольной силы в соответствующем сечении бруса.
В поле эпюры, в круге проставляется её знак, а рядом с эпюрой — её обозначение и размерность.
Как видно из построенной эпюры N, в местах приложения сосредоточенных сил R, F1 и F2 (сечения B, C и K) имеют место скачки по модулю на величину этих сил.
Так же заметим, что участки бруса, где значения N положительны (часть бруса CK) — растянуты, а где величина N отрицательна (BC) – сжаты.
Участок KM в данном случае не деформируется.
Расчет значений эпюры напряжений
Характер изменения нормальных напряжений по длине бруса будет таким же, как для продольной силы. Только в месте резкого изменения формы бруса (сечение D) на эпюре σ, в отличие от эпюры N, возникает скачок значений из-за изменения площади сечения A.
Вычислим напряжения на участках:
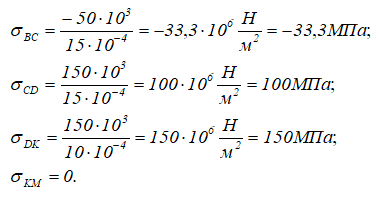
По рассчитанным значениям строим эпюру σ
Расчеты для построения эпюры перемещений
Определяем абсолютные деформации отдельных участков бруса по формуле
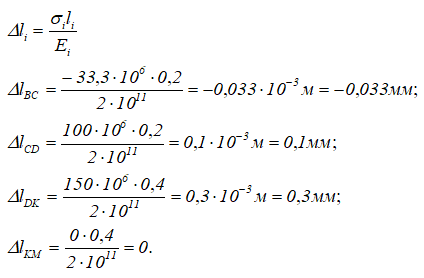
Вычисляем перемещения характерных сечений
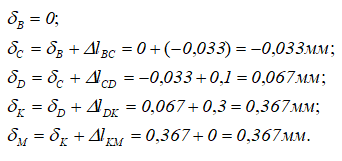
По результатам этих расчетов строим эпюру продольных перемещений
Как видно по эпюре, на участках бруса с нулевыми эпюрами продольных сил и напряжений, эпюра перемещений имеет постоянное значение.
Т.е. все точки данного участка перемещаются на одну и ту же величину.
Построение эпюр при действии продольной равномерно распределенной нагрузки
В случаях, когда на одном или нескольких участках стержня действует равномерно распределенная нагрузка q, эпюры внутренних сил и напряжений на этих участках будут ограничиваться прямой наклонной линией, а эпюра перемещений – параболой.
Задание
Для данного стержня, закрепленного вертикально, требуется:
1) построить эпюру продольных усилий – N;
2) построить эпюру нормальных напряжений – σ;
3) построить эпюру перемещений точек, лежащих на оси стержня – Δ;
Данные для решения задачи:
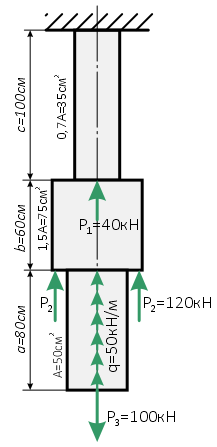
Внешние силы: P1=40кН, P2=120кН (удвоенная сила) и P3=100кН;
Продольная равномерно распределенная нагрузка q=50кН/м;
Базовая площадь сечения участков бруса: A=50см2;
Длина участков: a=80см, b=60см и c=100см.
Принять: модуль Юнга материала бруса E=1∙105МПа
Решение
Вычерчиваем заданную расчетную схему вертикального стержня в масштабе, указываем числовые значения приложенных нагрузок, площади поперечного сечения и продольные размеры.
Обозначаем силовые участки бруса цифрами 1, 2 и 3, а характерные сечения стержня, начиная от его заделки (буквами B, C, D и K).
Определим опорную реакцию стержня в заделке, направив её вниз.
Уравнение равновесия стержня
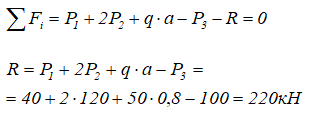
Положительное значение реакции означает, что выбранное направление оказалось верным.
Построение эпюры внутренних продольных усилий
Для наглядности, рассмотрим решение задачи с отрисовкой отсеченных частей бруса сечениями по участкам.
Стержень имеет 3 силовых участка.
Рассчитаем величину внутренних продольных сил N по каждому участку стержня методом сечений, рассматривая, например, всю нижнюю отсеченную часть бруса.
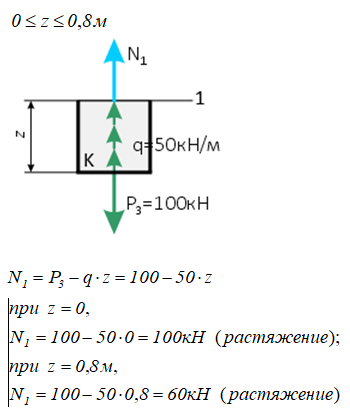
1 участок (DK)
2 участок (CD)
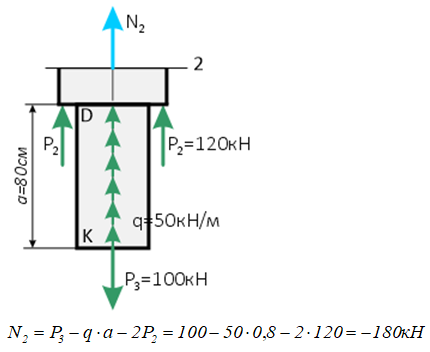
Внутренняя сила получилась отрицательной, следовательно, участок №2 сжимается.
3 участок (BC)
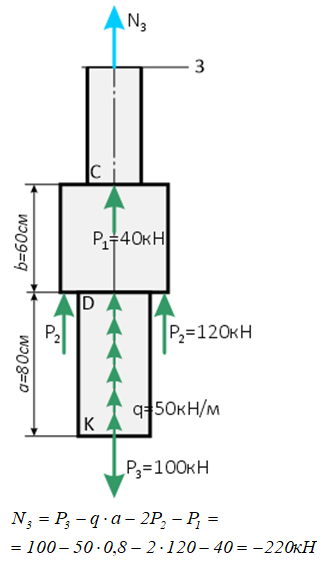
Внутреннее усилие на третьем участке по величине и знаку равно сжимающей опорной реакции R.
По полученным данным строим эпюру внутренних продольных сил N
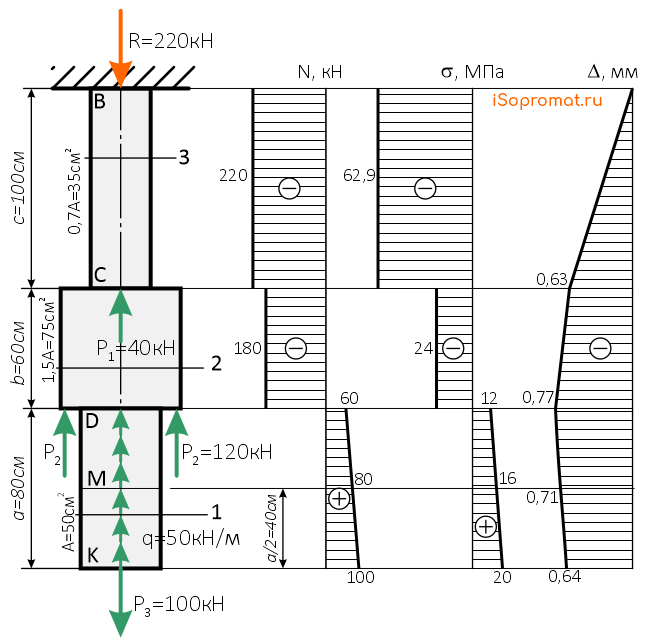
На эпюре скачки значений внутренней продольной силы в сечениях стержня, где приложены внешние силы, включая реакцию в опоре.
Эти скачки равны величине этих сил.
На 1 участке, где действует равномерно-распределенная нагрузка q, эпюра продольных усилий N ограничена наклонной прямой линией.
Следовательно, реакция в опоре и внутренние продольные силы определены верно, а эпюра построена правильно.
Расчет и построение эпюры нормальных напряжений
Рассчитаем значения напряжений
1 участок
На этом участке, согласно формулы, напряжения меняются по линейному закону.
Определим напряжения в крайних сечениях участка:
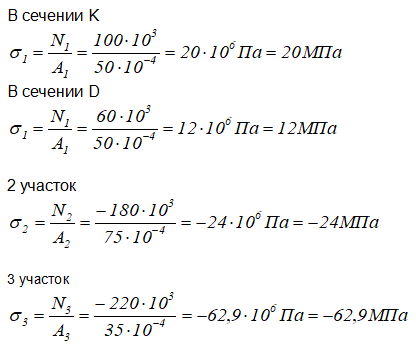
По полученным данным строим эпюру нормальных напряжений σ
Построение эпюры продольных деформаций при растяжении-сжатии
Выполним расчет продольных деформаций Δl участков стержня
1 участок
Удлинение 1 участка рассчитаем по среднему значению нормальных напряжений.
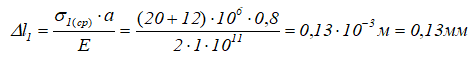
На этом участке, из-за действия распределенной нагрузки, внутренние силы и напряжения переменны по его длине, поэтому эпюра перемещений сечений будет иметь вид параболы.
Для построения параболы необходимы минимум 3 точки.
Для этого рассчитаем, например, деформацию нижней половины первого участка.
Внутренние продольные усилия в середине первого участка, при a/2 (в сечении M)
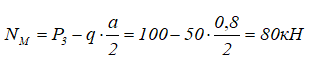
Нормальные напряжения в сечении M
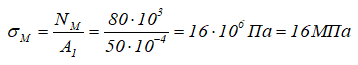
Деформация участка KM
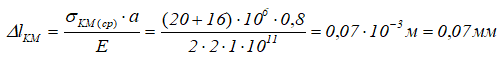
Тогда деформация участка DM
![]()
2 участок
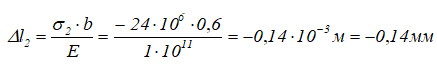
3 участок
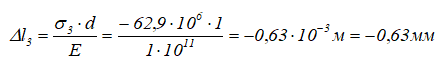
Расчет перемещений Δ характерных сечений стержня
В данной задаче сечение B является неподвижным, так как находится в заделке, поэтому
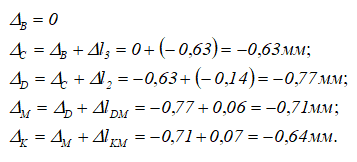
По этим данным строим эпюру продольных перемещений Δ сечений стержня.
Обратите внимание на то, что между эпюрами напряжений и перемещений есть дифференциальная зависимость.
При этом необходимо учесть, что на участках без распределенной нагрузки эпюра Δ меняется по линейному закону, в то время как на участке 1 меняется по параболе.
Полное изменение длины стержня можно определить, сложив с учётом знаков, деформации всех участков стержня.
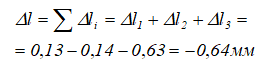
В результате деформаций, общая длина стержня уменьшится на 0,64мм.
Это значение должно совпадать с перемещением самого нижнего сечения стержня на эпюре перемещений.
Построение эпюр нормальных сил и напряжений при растяжении и сжатии с учетом собственного веса стержней
В задачах данного типа, собственный вес учитывается в виде распределенной нагрузки, с интенсивностью равной произведению удельного веса материала и площади поперечного сечения.
Задача
Стальной стержень (модуль упругости E=200ГПа) находится под действием продольной силы P и собственного веса (γ=7,8т/м3).
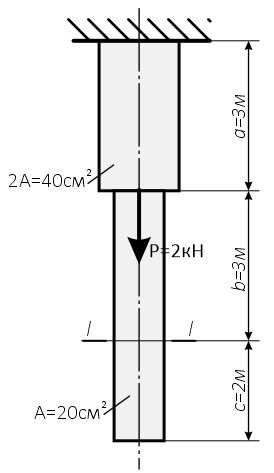
Требуется построить эпюры внутренних продольных усилий N и напряжений.
Найти полное перемещение сечения I-I.
A=20см2; a=3,0м; b=3,0м; с=2,0м; P=2кН.
Решение задачи
Переведем собственный (удельный) вес материала γ из т/м3 в Н/м3
![]()
Расчет и построение эпюры нормальных сил
Определяем нормальные силы N по участкам стержня:
1 участок (AC)
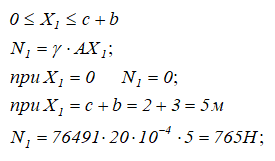
2 участок (CD)
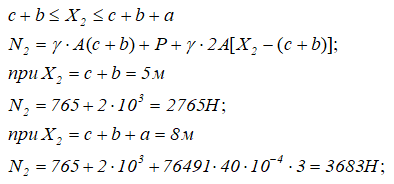
Расчет продольных напряжений для построения их эпюры
Определяем значения нормальных напряжений σ по участкам:
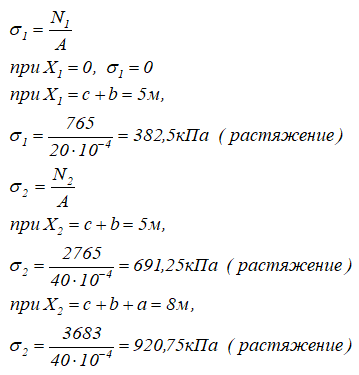
Строим эпюры нормальных сил и напряжений.
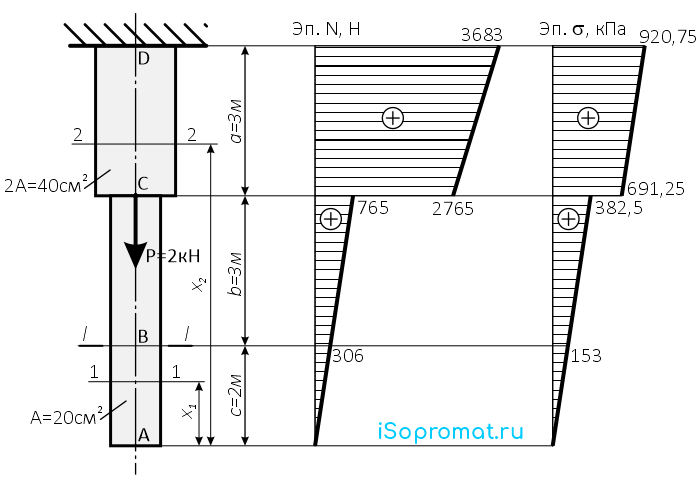
Рассчитаем значения нормальных сил N и напряжений σ в сечении I-I
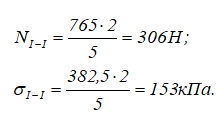
Определяем перемещение сечения I-I:
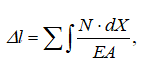
За начало отсчета перемещений принимаем сечение D, так как оно закреплено в жесткой заделке.
Все сечения стержня перемещаются вниз, т.к. согласно эпюры N все участки стержня растягиваются.
Перемещение сечения C:
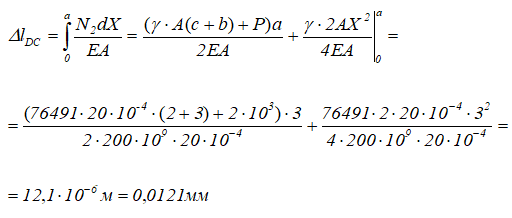
Перемещение сечения I-I является алгебраической суммой перемещения сечения C (ΔlDC) и удлинения части стержня CB длиной b.
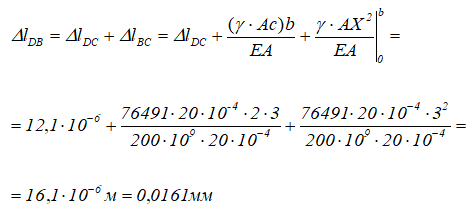
Таким образом, сечение I-I переместилось вниз на 0,0161мм.
Эпюра линейных перемещений точек бруса рассчитывается и строится аналогично эпюре Δ из предыдущего примера.
Далее: