Пример решения задачи по расчету методом начальных параметров (МНП) линейных вертикальных (прогиб) и угловых (угол наклона) перемещений сечений двухопорной, статически определимой балки, при её деформации под действием заданной системы внешних нагрузок.
Задача:
Для заданной стальной двухопорной балки (рис. 1), нагруженной изгибающим моментом m, сосредоточенной силой F и равномерно распределенной нагрузкой q, требуется методом начальных параметров, определить вертикальное перемещение (прогиб) сечений балки в точках B и D, и угловые перемещения сечений на опорах (в точках A и C).
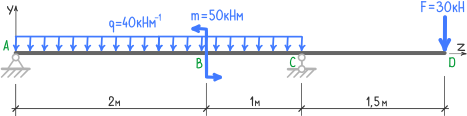
Рис. 1
Характеристики материала и сечения балки:
Материал балки — сталь, для которой модуль упругости I рода равен 200 ГПа.
Сечение балки — двутавр №45, осевой момент инерции которого по сортаменту двутавров Ix=3800см4.
Пример решения
Предыдущие этапы решения задачи:
Покажем найденные ранее реакции опор:
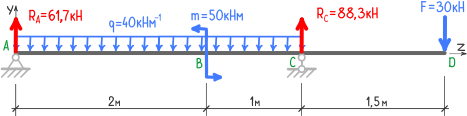
Методом начальных параметров можно рассчитывать только прямые балки постоянного сечения, выполненные по всей длине из одного материала.
Для расчета перемещений нам потребуется составить два уравнения метода начальных параметров (МНП).
Первое уравнение — для расчета угла наклона θ (тета) сечений балки, второе — для определения их вертикального перемещения (по оси y).
Уравнения МНП
Составление уравнений метода начальных параметров для балки в нашем видеоуроке:
Уравнения составляются по следующим шаблонам:
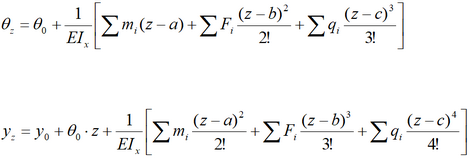
Здесь:
θz и yz — это соответственно поворот и прогиб рассматриваемого сечения балки расположенного на расстоянии z от начала координат;
θ0 и y0 — это угловое и вертикальное перемещения сечения балки в начале координат.
Собственно, это и есть начальные параметры;
В знаменателе перед скобкой — изгибная жесткость поперечного сечения балки, которая определяется произведением модуля Юнга и осевого момента инерции профиля;
Далее, m, F и q — это нагрузки, приложенные к балке, включая опорные реакции и компенсирующую распределенную нагрузку (если она есть);
Буквами a и b обозначаются расстояния от начала координат до соответствующих изгибающих моментов и сосредоточенных сил;
«c» — расстояние от начала координат до сечения, где начинает действовать распределенная нагрузка.
z — положение рассматриваемого сечения балки.
Подготовка к расчету
Перед составлением уравнений МНП для заданной балки неоюходимо выполнить два действия:
За начало координат выбирается крайнее левое или крайнее правое сечение балки.
При этом хорошо, если это сечение располагается на опоре.
В этом случае, прогиб балки в начале координат у0 будет равен нулю.
В данном примере, на опоре располагается левый конец балки.
Поэтому за начало координат выберем точку A.
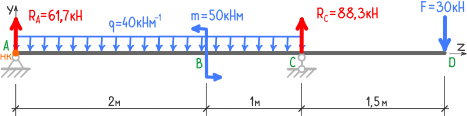
2. В случае, когда действие распределенной нагрузки обрывается, не доходя до конца балки, её действие необходимо продлить до конца, и на этом же участке добавляется компенсирующая нагрузка той же величины, но обратного направления.
Это делается потому, что значение «c» в уравнениях МНП учитывает только начало действия нагрузки.
В данной схеме, распределенная нагрузка q, начинаясь в точке A, продолжается только до сечения C, поэтому продляем её действие до конца балки (точки D)
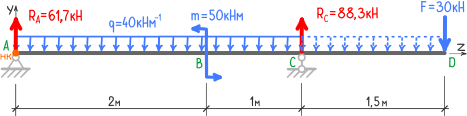
и, чтобы вернуться к исходной схеме нагружения, на этой же длине (CD) добавляем компенсирующую нагрузку q, направленную вверх.
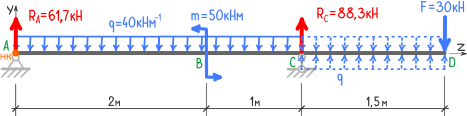
Теперь можно переходить к составлению уравнений метода начальных параметров.
Составление уравнений МНП для балки
Уравнения МНП записываются последовательно по каждому силовому участку от начала координат.
Нагрузки в уравнения записываются с учетом их знака по правилу знаков для изгибающих моментов:
Нагрузки, сжимающие верхние слои балки записываются положительными, а сжимающие нижние слои — отрицательными.
Составим уравнение угловых перемещений θz:
Переписываем часть уравнения до скобки без изменений и открываем скобку.

Здесь будут записаны нагрузки по участкам, начиная с первого от начала координат.
Для удобства можно мысленно провести сечение участка.
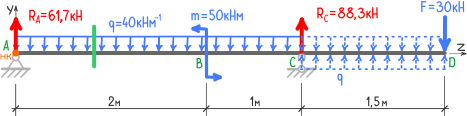
Смотрим в сторону начала балки, и видим опорную реакцию RA и распределенную нагрузку q.
RA стремится сжать верхние слои балки, поэтому записывается положительной, нагрузка q отрицательна, т.к. сжимает нижние слои балки.

b и c — расстояния от начала координат до соответственно реакции опоры и начала нагрузки, здесь равны нулю.
Обратите внимание: записав в уравнение МНП распределенную нагрузку на этом участке, мы записали всю верхнюю нагрузку целиком. По каждому участку ее записывать не нужно.
Так как слева от сечения нагрузок больше нет, отделяем эту часть уравнения и показываем, что она будет справедлива для всех сечений балки от точки A до точки B включительно.
Переходим на второй силовой участок балки от начала координат.
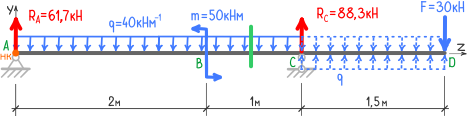
Здесь так же, можно провести мысленное сечение между точками B и C и глядя в сторону начала балки, видим, что добавляется изгибающий момент m, который стремится сжать нижние слои балки.
Записываем его с минусом в следующем виде.
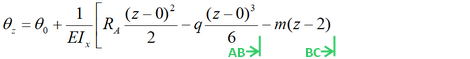
Получилось уравнение для расчета угловых перемещений для всех точек второго силового участка балки.
Переходим на третий.
Проводим сечение, и смотрим в сторону начала координат.
Добавляем вторую реакцию RC и компенсирующую (нижнюю) распределенную нагрузку q.
По правилу знаков, они будут положительными.
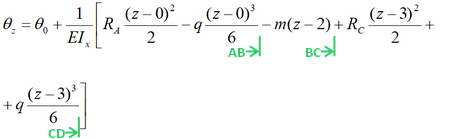
Получаем уравнение для третьего участка и закрываем скобку.
Силу F, приложенную в точке D не записываем.
Сосредоточенные силы и моменты, приложенные к концу балки, в уравнениях не участвуют.
В данном методе, они оказывают влияние на деформацию балки через опорные реакции.
Уравнение прогибов балки составляется аналогично.
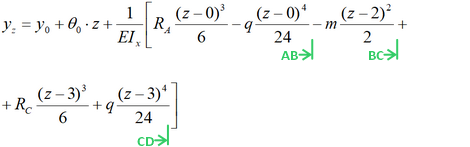
В полученные уравнения подставляем все имеющиеся данные и значения.
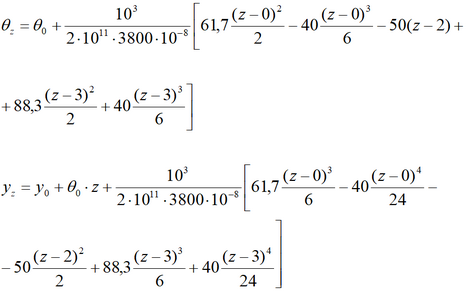
Общую для всех нагрузок, кратную приставку «кило» выносим за скобки, и можно еще немного сократить выражения.

Переменную z мы будем задавать сами, поэтому в уравнениях для заданной балки остаются неизвестными только начальные параметры θ0 и y0.
Нахождение начальных параметров
Начальные параметры определяются из граничных условий, по способу закрепления балки в опорах.
Рассматривая двухопорную балку, мы точно знаем, что при ее деформации, сечения расположенные на шарнирных опорах, по вертикали не перемещаются.
Другими словами, прогибы балки в точках A и C равны нулю.
Запишем граничные условия:
yA=yz=0=0=y0
yC=yz=3м=0
Из первого условия следует, что рационально выбрав начало координат, мы сразу получили значение y0. Здесь оно равно нулю, т.к. нулевое сечение находится на опоре.
Второе условие используем для нахождения второго начального параметра θ0.
Запишем уравнение прогибов для точки C, приравняв его к нулю и подставив соответствующее значение z.
![]()
Откуда находим значение поворота сечения в начале координат.
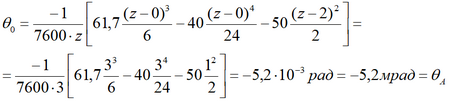
Поворот сечения получаем в радианах, вертикальное перемещение — в метрах.
Для консольных балок, начало координат однозначно следует выбирать в заделке. В этом случае нулю будут равны оба начальных параметра.
Теперь, когда известны все данные, можно рассчитать искомые перемещения сечений, выбирая соответствующую часть уравнений и подставляя координату z рассматриваемой точки.
Расчет перемещений сечений балки
Для нахождения прогиба в точке B берем часть уравнения метода начальных параметров для первого участка и z равную 2 метра.
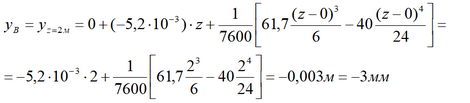
Для точки D записываем уравнение целиком и подставляем вместо z всю длину балки.
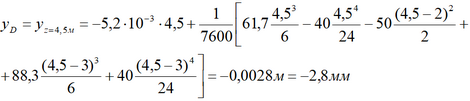
Аналогично, используя первое уравнение, определяем углы наклона сечений на опорах.
Угловое перемещение сечения на левой опоре уже найдено при расчете начальных параметров
θA=θz=0=θ0=-5,2 мрад.
Наклон сечения на правой опоре, в т. C
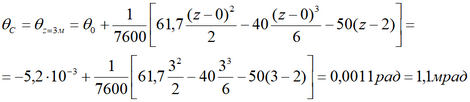
По этим данным строим линию изогнутой оси балки или эпюру перемещений.
Далее: