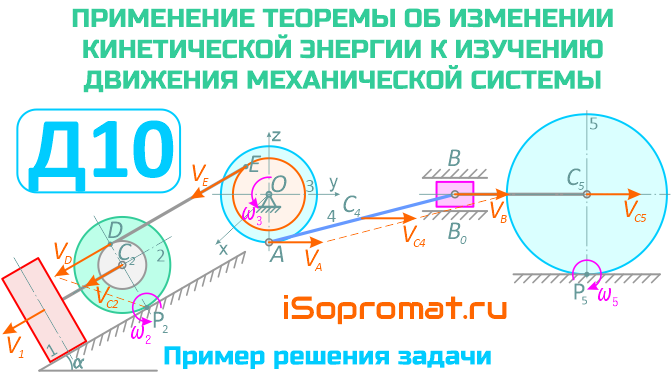
Пример решения задачи РГР Д10 по определению скорости тела (груза) механической системы в тот момент, когда пройденный им путь станет равным значению s, учитывая трение скольжения и сопротивление качению тела, но пренебрегая другими силами сопротивления.

Задача

Механическая система под действием сил тяжести приходит в движение из состояния покоя.

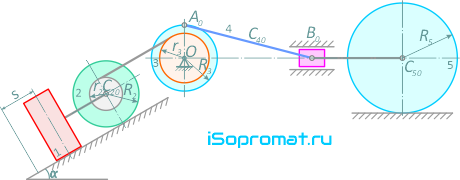
Учитывая трение скольжения тела 1 и сопротивление качению тела 5, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s.

Дано: m₁ – масса груза 1, m₂=2m₁, m₃=m₁, m₄=0,5m₁, m₅=20m₁, R₂=R₃=12см, r₂=0,5R₂, r₃=0,75R₃, R₅=20 см, AB=l=4R₃, i_2ξ=8см, i_3x=10см, α=30°, ƒ=0,1, δ=0,2см, s=0,06π м.

Сопротивление качению тела 2 не учитывать. Шатун 4 считать тонким однородным стержнем; каток 5 – однородный сплошной цилиндр. Массами звена BC₅ и ползуна B пренебречь. На рисунке 2, а показана механическая система в начальном положении.

Найти: ν₁ – скорость груза 1 в конечном положении.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Применим теорему об изменении кинетической энергии системы:

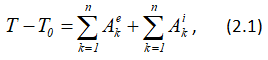
где T₀ и T – кинетическая энергия системы в начальном и конечном положениях; ∑A_k^e – сумма работ внешних сил, приложенных к системе, на перемещении системы из начального положения в конечное; ∑A_kⁱ – сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями и стержнями, ∑A_kⁱ = 0.

Так как в начальном положении система находится в покое, то T₀=0.

Следовательно, уравнение (2.1) принимает вид

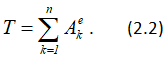
Для определения кинетической энергии T и суммы работ внешних сил изобразим систему в конечном положении (рисунок 2.1, б, в).

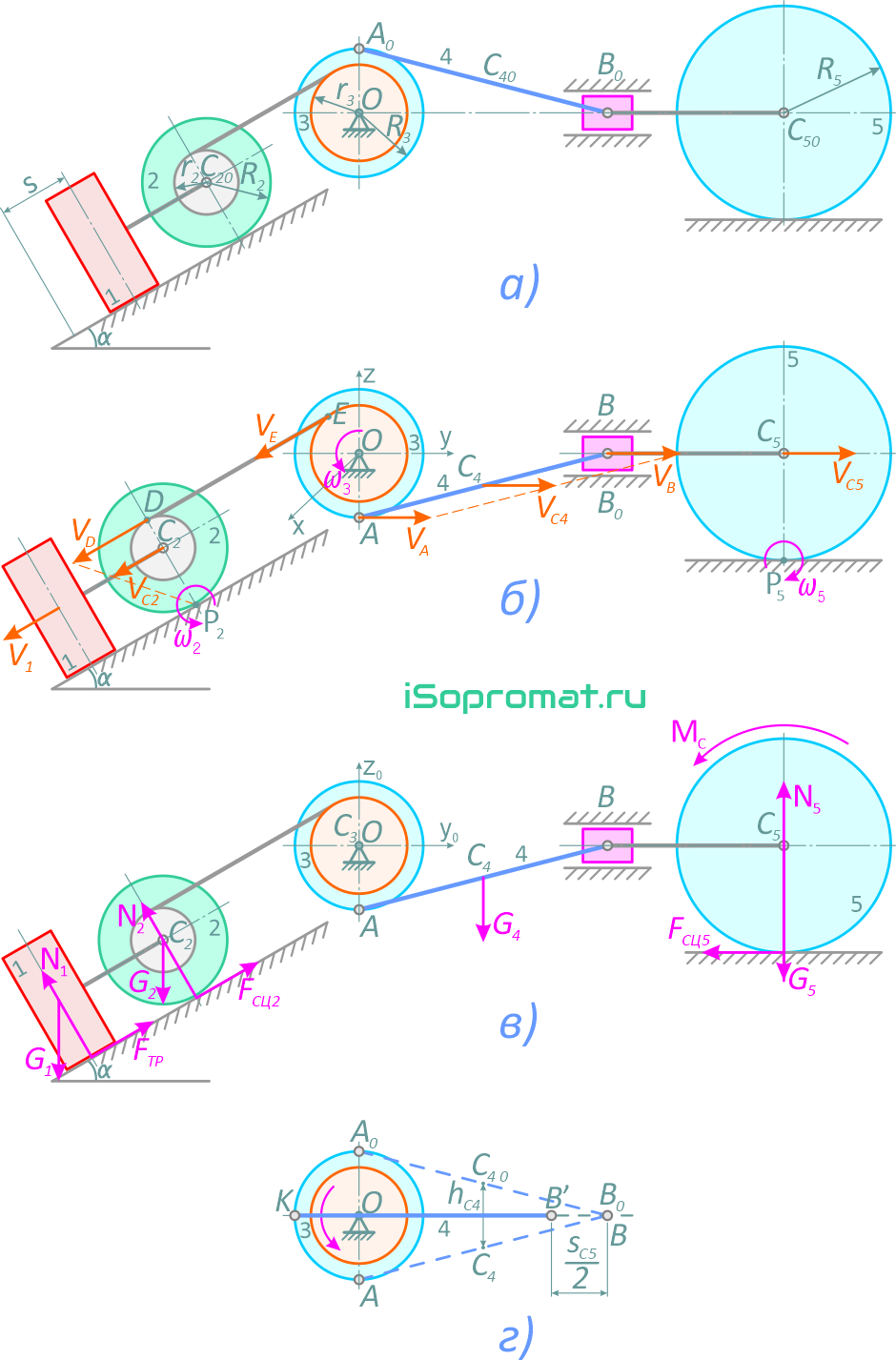
Напишем кинематические соотношения между скоростями и перемещениями точек системы, т.е. уравнения связей, при этом скорости и перемещения выразим соответственно через скорости и перемещения груза 1.

Скорость центра масс C катка 2 равна скорости груза 1:

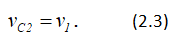
Угловая скорость катка 2, мгновенный центр скоростей которого находится в точке P₂,

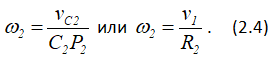
Скорость точки D катка 2

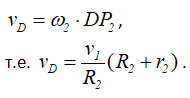
Скорость точки E блока 3 равна скорости точки D катка 2:

Но v_E = ω₃r₃. Следовательно, по (2.5),

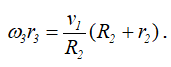
Так как R₂ = 2r₂, то

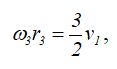
откуда

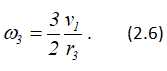
Заменяя в формуле (2.6)

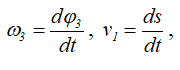
получим

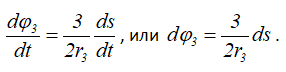
После интегрирования (при нулевых начальных условиях)

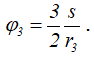
Когда груз 1 пройдет путь s = 0,06π м, блок 3 повернется на угол φ₃:

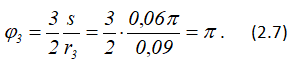
При этом повороте блока 3 на 180º его точка A₀ перейдет в конечное положение A и шатун 4 из начального положения A₀B₀ перейдет в конечное положение AB.

Каток 5 переместится влево при повороте блока 3 на угол π/2 и вправо при повороте блока еще на π/2; значит, конечное положение катка 5 совпадает с его начальным положением.

Таким образом, конечное положение всей системы вполне определено (рисунок 2.1, б).

Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3, 4, 5:

Кинетическая энергия груза 1, движущегося поступательно,

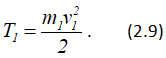
Кинетическая энергия катка 2, совершающего плоское движение,

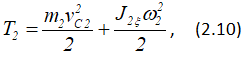
где J_2ξ — момент инерции катка 2 относительно его продольной центральной оси C_2ξ:

Подставляя (2.3), (2.4), (2.11) в формулу (2.10), получаем

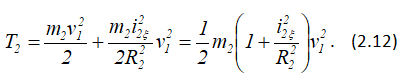
Кинетическая энергия тела 3, вращающегося вокруг оси Ox,

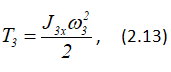
где J_3x — момент инерции блока 3 относительно оси Ox:

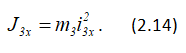
Подставляя (2.6), (2.14) в формулу (2.13), получаем

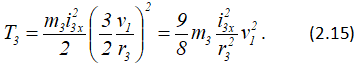
Кинетическая энергия шатуна 4, совершающего плоское движение,

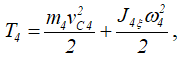
где v_C4 — скорость центра масс C₄ шатуна 4; ω₄ — угловая скорость шатуна 4; J_4ξ — момент инерции шатуна относительно центральной оси C_4ξ.

Для определения v_C4 и ω₄ найдем положение мгновенного центра скоростей шатуна 4. Так как скорости точек A и B в этот момент параллельны, то мгновенный центр скоростей шатуна 4 находится в бесконечности; следовательно, угловая скорость шатуна в данный момент ω₄=0, а скорости всех его точек параллельны и равны между собой. Таким образом, кинетическая энергия шатуна 4

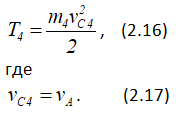
Вращательная скорость точки A тела 3

или с учетом (2.14)

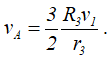
Поскольку r₃ = 3/4 R₃, получим v_A = 2v₁.

После подстановки (2.19) в (2.16) выражение кинетической энергии шатуна 4 принимает вид

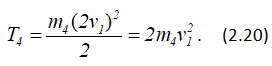
Кинетическая энергия катка 5, совершающего плоское движение,

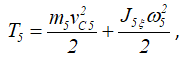
где v_C5 — скорость центра масс C₅ катка 5; ω₅ — угловая скорость катка 5; J_5ξ — момент инерции катка 5 (однородного сплошного цилиндра) относительно его центральной оси C_5ξ, J_5ξ = m₅R₅²/2.

Так как каток катится без скольжения, то мгновенный центр скоростей находится в точке P₅.
Поэтому ω₅ = v_C5/R₅.

Следовательно,

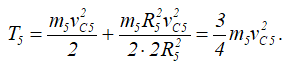
Так как звено BC₅ совершает поступательное движение, то v_C5 = v_B, но v_B = v_C4 = 2v₁. Значит, v_C5 = 2v₁.

Поэтому выражение кинетической энергии катка 5 принимает вид

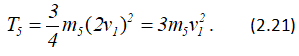
Кинетическая энергия всей механической системы определяется по формуле (2.8) с учетом (2.9), (2.12), (2.15), (2.20) и (2.21):

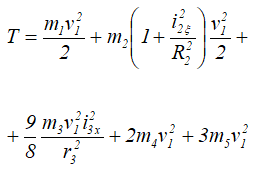
Подставляя сюда заданные значения масс, получаем

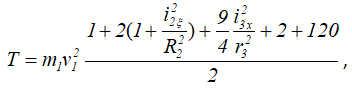
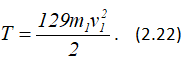
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном её перемещении (внешние силы, приложенные к системе, показаны на рисунке 2.1, в).

Работа силы тяжести G₁

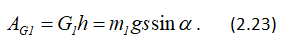
Работа силы трения скольжения F_тр

Так как

то

Работа силы тяжести G₂

Работа сил сцепления F_сц2, F_сц5 катков 2 и 5 равна нулю, т.к. эти силы приложены в мгновенных центрах скоростей этих катков.

Работа силы тяжести G₄

где h_С4 — вертикальное перемещение центра тяжести С₄ шатуна 4 из начального положения в его конечное положение (рисунок 2.1, г), h_С4 = R₃:

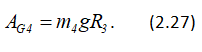
Работа пары сил сопротивления качению катка 5

где M_C = δN₅ = δG₅ — момент сопротивления качению катка 5; φ₅ — угол поворота катка 5.

Так как каток 5 катится без скольжения, то угол его поворота

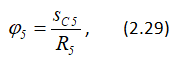
где s_C5 — перемещение центра тяжести C₅ катка 5.

В данном примере работу пары сил сопротивления вычислим как сумму работ этой пары при качении катка 5 влево при повороте тела 3 на угол π/2 и качении вправо, когда тело 3 повернется еще на угол π/2. Перемещение центра тяжести C₅ катка 5 равно перемещению ползуна B влево и вправо:

Определим перемещение B₀B’ при повороте тела 3 на угол π/2. За начало отсчета координаты точки B выберем неподвижную точку K плоскости (рисунок 2.1, г). При этом повороте тела 3 шатун из положения A₀B₀ перейдет в положение KB’.

Тогда

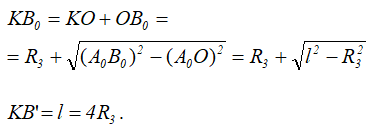
Следовательно,

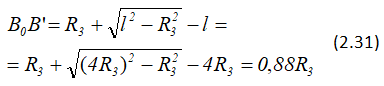
Подставляя (2.31) и (2.30), а затем в (2.29), находим полный угол поворота катка 5:

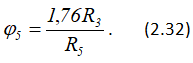
Работа момента сопротивления качению по (2.28)

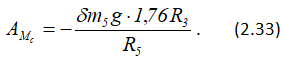
Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (2.23) – (2.27) и (2.33):

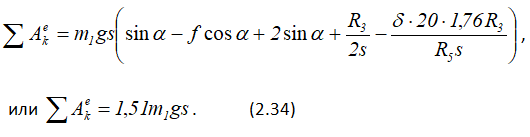
Согласно теореме (2.2), приравняем значения T и ΣA_k^e, определяемые по формулам (2.22) и (2.34):

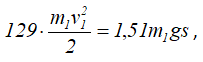
откуда v₁ = 0,21 м/с.

Другие примеры решения задач >